题目内容
 已知O为坐标原点,M(cosx,2
已知O为坐标原点,M(cosx,2| 3 |
| ||
| 6 |
| OM |
| ON |
(1)求函数y=f(x)的表达式;
(2)若角C∈[
| π |
| 3 |
(3)在(2)的条件下,试画出y=f(x)(x∈[0,π])的简图.
分析:(1)利用向量的坐标运算与辅助角公式可得y=f(x)=2sin(2x+
)+a+1;
(2)由
≤C<π,可得2C+
∈[
,
],依题意得,2×(-1)+a+1=0,从而可求得a;
(3)当x∈[0,π]时,作出函数y=2sin(2x+
)+2图象即可.
| π |
| 6 |
(2)由
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 13π |
| 6 |
(3)当x∈[0,π]时,作出函数y=2sin(2x+
| π |
| 6 |
解答:解:(1)y=f(x)=2cos2x+2
(sinxcosx+
a)
=cos2x+
sin2x+1+a
=2sin(2x+
)+a+1
(2)∵
≤C<π,故2C+
∈[
,
],
∴y=f(C)=2sin(2C+
)+a+1的最小值为:2×(-1)+a+1=0,
∴a=1.
(3)由(2)可知:y=2sin(2x+
)+2,
∵0≤x≤π,
∴
≤2x+
≤
,0≤y≤4.图象如下:
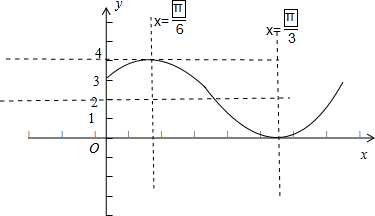
| 3 |
| ||
| 6 |
=cos2x+
| 3 |
=2sin(2x+
| π |
| 6 |
(2)∵
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 13π |
| 6 |
∴y=f(C)=2sin(2C+
| π |
| 6 |
∴a=1.
(3)由(2)可知:y=2sin(2x+
| π |
| 6 |
∵0≤x≤π,
∴
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |

点评:本题考查平面向量数量积的运算,并以平面向量数量积为载体考查三角函数的化简求值,考查正弦函数的图象与性质,突出考查作图能力,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 已知O为坐标原点,
已知O为坐标原点, ),N(2cosx,sinxcosx+
),N(2cosx,sinxcosx+ a),其中x∈R,a为常数,设函数
a),其中x∈R,a为常数,设函数 ,
,