题目内容
【题目】如图所示,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() 作直线
作直线![]() 交椭圆于不同两点
交椭圆于不同两点![]() ,
,![]() .
.
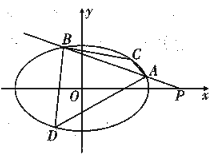
(1)求椭园的方程;
(2)①设直线的斜率为![]() ,求出与直线
,求出与直线![]() 平行且与椭圆相切的直线方程(用
平行且与椭圆相切的直线方程(用![]() 表示);
表示);
②若![]() ,
,![]() 为椭圆上的动点,求四边形
为椭圆上的动点,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)由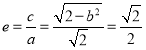 求出
求出![]() 即可
即可
(2)①设切线方程为![]() ,然后与椭圆的方程联立消元,利用
,然后与椭圆的方程联立消元,利用![]() 得出
得出![]() 即可
即可
②要使得四边形![]() 的面积最大,需满足
的面积最大,需满足![]() ,
,![]() 两点到直线
两点到直线![]() 的距离之和最大,即两条切线间的距离
的距离之和最大,即两条切线间的距离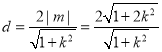 最大,然后算出弦长
最大,然后算出弦长![]() ,然后可得四边形
,然后可得四边形![]() 的面积
的面积![]()
![]()
![]() ,即可得出答案.
,即可得出答案.
(1)椭圆![]() 中,
中,
![]() ,
,![]() ,
,
![]() 椭圆的离心率为
椭圆的离心率为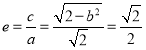 ,解得
,解得![]() ,
,
![]() 椭圆的方程为
椭圆的方程为![]() .
.
(2)①设切线方程为![]() ,
,
代入![]() ,可得
,可得![]() ,
,
由![]() ,可得
,可得![]() ,故切线方程为
,故切线方程为![]() .
.
②要使得四边形![]() 的面积最大,需满足
的面积最大,需满足![]() ,
,![]() 两点到直线
两点到直线![]() 的距离之和最大,
的距离之和最大,
即两条切线间的距离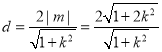 最大.
最大.
设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立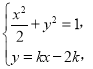 整理得
整理得![]() ,
,
则![]() ,
,![]() ,
,
故![]() ,
,
故四边形![]() 的面积
的面积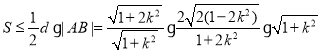
![]()
![]() ,
,
当且仅当![]() ,且
,且![]() ,
,![]() 或
或![]() ,
,![]() 时等号成立.
时等号成立.
故所求最大值为![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目