题目内容
15.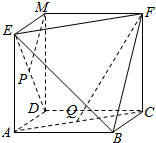 如图所求,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点.
如图所求,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点.求:
(1)$\overrightarrow{PM}$与$\overrightarrow{FQ}$所成的角;
(2)P点到平面EFB的距离;
(3)异面直线PM与FQ的距离.
分析 (1)以D为坐标原点,DA为x轴,DC为y轴,DM为z轴,建立空间直角坐标系,求出$\overrightarrow{PM}$与$\overrightarrow{FQ}$的坐标,再利用向量的夹角公式求出两向量所成的角;
(2)设$\overrightarrow{n}$=(x,y,z)是平面EFB的单位法向量,根据条件建立方程组,求出$\overrightarrow{n}$,设所求距离为d,利用d=|$\overrightarrow{PE}$•$\overrightarrow{n}$|=进行求解即可.
(3)求出两异面直线的公垂线上的方向向量,即可求出异面直线PM与FQ的距离.
解答 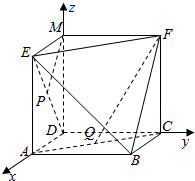 解:建立空间直角坐标系,使得D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、M(0,0,a)、E(a,0,a)、F(0,a,a),则由中点坐标公式得P($\frac{a}{2}$,0,$\frac{a}{2}$)、Q($\frac{a}{2}$,$\frac{a}{2}$,0).
解:建立空间直角坐标系,使得D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、M(0,0,a)、E(a,0,a)、F(0,a,a),则由中点坐标公式得P($\frac{a}{2}$,0,$\frac{a}{2}$)、Q($\frac{a}{2}$,$\frac{a}{2}$,0).
(1)∴$\overrightarrow{PM}$=(-$\frac{a}{2}$,0,$\frac{a}{2}$),$\overrightarrow{FQ}$=($\frac{a}{2}$,-$\frac{a}{2}$,-a),
$\overrightarrow{PM}$•$\overrightarrow{FQ}$=(-$\frac{a}{2}$)×$\frac{a}{2}$+0+$\frac{a}{2}$×(-a)=-$\frac{3}{4}$a2,且|$\overrightarrow{PM}$|=$\frac{\sqrt{2}}{2}$a,|$\overrightarrow{FQ}$|=$\frac{\sqrt{6}}{2}$a.
∴cos<$\overrightarrow{PM}$,$\overrightarrow{FQ}$>=$\frac{-\frac{3}{4}{a}^{2}}{\frac{\sqrt{2}}{2}a×\frac{\sqrt{6}}{2}a}$=-$\frac{\sqrt{3}}{2}$.
故得两向量所成的角为150°.
(2)设$\overrightarrow{n}$=(x,y,z)是平面EFB的单位法向量,即|$\overrightarrow{n}$|=1,$\overrightarrow{n}$⊥平面EFB,
∵$\overrightarrow{EF}$=(-a,a,0),$\overrightarrow{EB}$=(0,a,-a),
∴有$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}+{z}^{2}=1}\\{-ax+ay=0}\\{ay-az=0}\end{array}\right.$,
∴$\overrightarrow{n}$=($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$),$\overrightarrow{PE}$=($\frac{a}{2}$,0,$\frac{a}{2}$).
设所求距离为d,则d=|$\overrightarrow{PE}$•$\overrightarrow{n}$|=$\frac{\sqrt{3}}{3}$a.
(3)设$\overrightarrow{e}$=(x1,y1,z1)是两异面直线的公垂线上的方向向量,则由$\overrightarrow{PM}$=(-$\frac{a}{2}$,0,$\frac{a}{2}$),$\overrightarrow{FQ}$=($\frac{a}{2}$,-$\frac{a}{2}$,-a),
得求得其中的一个$\overrightarrow{e}$=(1,-1,1),
而$\overrightarrow{MF}$=(0,a,0).设所求距离为m,则m=$\frac{|\overrightarrow{MF}•\overrightarrow{m}|}{|\overrightarrow{m}|}$=$\frac{\sqrt{3}}{3}$a.
点评 本题主要考查了异面直线及其所成的角,以及点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | “a≤b”是“a+c≤b+c”的充分不必要条件 | |
| B. | “已知x,y∈R,且x+y≠6,则x≠2或y≠4”是真命题 | |
| C. | 命题“?x∈R,2x>0”的否定是“?x∈R,2x<0” | |
| D. | “若x2-1=0,则x=1或x=-1”的否命题为“x2-1≠0或x≠-1” |
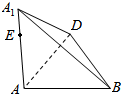 如图,在三棱锥A1-ABC中,A1A=AB=AD=2,A1A⊥平面ABD,∠DAB=90°,AE=$\frac{4}{3}$,动点F在△A1BD(包括边界)上运动,则AF+EF的最小值为( )
如图,在三棱锥A1-ABC中,A1A=AB=AD=2,A1A⊥平面ABD,∠DAB=90°,AE=$\frac{4}{3}$,动点F在△A1BD(包括边界)上运动,则AF+EF的最小值为( )| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 四棱锥S-ABCD中,底面边长为2,侧棱长为3,E是侧棱SC的中点,建立如图所示的空间直角坐标系,试求点A、C、E的坐标.
四棱锥S-ABCD中,底面边长为2,侧棱长为3,E是侧棱SC的中点,建立如图所示的空间直角坐标系,试求点A、C、E的坐标.