题目内容
当m取什么实数时,方程4x 2+(m-2)x+(m-5)=0分别有:(1)两个实根;(2)一正根和一负根;(3)正根绝对值大于负根绝对值;(4)两根都大于1.
解析:解这类题要充分利用判别式和韦达定理.
答案:设方程4x 2+(m-2)x+(m-5)=0的两根为x 1、x 2,
(1)若方程4x 2+(m-2)x+(m-5)=0有两个正根,则需满足?
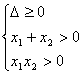
![]()
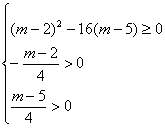
![]()
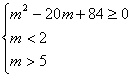
![]()
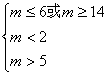
![]() m∈
m∈![]() .
.
∴此时m的取值范围是![]() ,即原方程不可能有两个正根.
,即原方程不可能有两个正根.
(2)若方程4x 2+(m-2)x+(m-5)=0有一正根和一负根,则需满足?
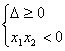
![]()
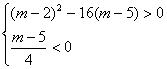
![]() m<5.
m<5.
∴此时m的取值范围是(-∞,5).?
(3)若方程4x 2+(m-2)x+(m-5)=0的正根绝对值大于负根绝对值,则需满足?
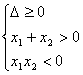
![]()
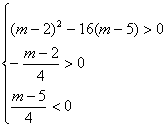
![]() m<2.
m<2.
∴此时m的取值范围是(-∞,2).?
(4)正解:若方程4x 2+(m-2)x+(m-5)=0的两根都大于1,则需满足?
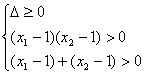
![]()
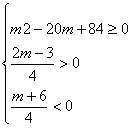
![]() m∈
m∈![]() .
.
∴此时m的取值范围是![]() ,即原方程不可能两根都大于1.
,即原方程不可能两根都大于1.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目