题目内容
当m取何实数时，方程2 (m+1)x2+4mx+3m－2=0(1) 有一正实根和一负实根；
(2) 有两个负实根；
(3) 正根绝对值大于负根绝对值；
(4) 有实根．
答案：
解析：
解析：
(1) 的充要条件是
(2) 的充要条件是 (3) 的充要条件是 (4) 当m+1=0，即m=－1时，原方程化为4x+5=0，故 当m≠－1时，方程有实根的充要条件是
综上，－2≤m≤1时，方程有实根．
|
且m≠－1
练习册系列答案
相关题目
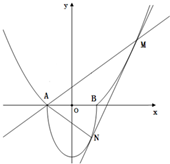如图，A（-1，0），B（1，0），过曲线C1：y=x2-1（|x|≥1）上一点M的切线l，与曲线
如图所示的曲线C是由部分抛物线C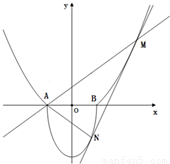
如图，A（-1，0），B（1，0），过曲线C1：y=x2-1（|x|≥1）上一点M的切线l，与曲线
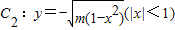也相切于点N，记点M的横坐标为t（t＞1）．