题目内容
已知![]() 直线
直线![]() 与函数
与函数![]() 、
、![]() 的图象都相切,且与函数
的图象都相切,且与函数![]() 的图象的切点的横坐标为1.(1)求直线
的图象的切点的横坐标为1.(1)求直线![]() 的方程和
的方程和![]() 的值; (2)若
的值; (2)若![]()
![]() ,求函数
,求函数![]() 的最大值;(3)当
的最大值;(3)当![]() 时,求证:
时,求证:![]()
(1)![]() (2)最大值
(2)最大值![]() - (3)略
- (3)略
解析:
:(1)把![]() 代入
代入![]() 得,
得,![]() 即直线
即直线![]() 切曲线
切曲线![]() 于点
于点![]() 故直线
故直线![]() 的方程为
的方程为![]()
设直线![]() 切曲线
切曲线![]() 于点
于点![]()
则![]() .由
.由![]()
![]()
![]() 得,
得,
![]() .将
.将![]() 代入得,
代入得, ![]()
解得,![]() 取
取![]() --5分
--5分
(2) 因为![]()
所以![]() 当
当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]() 因此
因此![]() 在
在![]() 上单增, 在
上单增, 在![]() 上单减.
上单减.
于是![]() 取得最大值
取得最大值![]() ---9分
---9分
(3)由(2)知,当![]() 时,
时, ![]() 即
即![]() 因此当
因此当![]() 时,有
时,有![]() .
.

练习册系列答案
相关题目
 则
则 ;②已知直线
;②已知直线 与函数
与函数 ,
,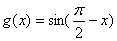 的图象分别交于
的图象分别交于 两点,则
两点,则 的最大值为
的最大值为 ;
; 是△
是△ 的两内角,如果
的两内角,如果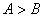 ,则
,则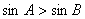 ;
; 。
。 则
则 ;②已知直线
;②已知直线 与函数
与函数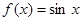 ,
, 的图象分别交于
的图象分别交于 两点,则
两点,则 的最大值为
的最大值为 ;
;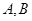 是△
是△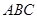 的两内角,如果
的两内角,如果 ,则
,则 ;
; 。
。 ,
, ,直线
,直线 与函数
与函数 、
、 的图象都相切,且与函数
的图象都相切,且与函数 .
. 的值;
的值; (其中
(其中 是
是 的最大值;
的最大值; 时,求证:
时,求证: .
.