题目内容
设双曲线C：
－y2＝1(a＞0)与直线l：x＋y＝1相交于两个不同的点A、B．
(Ⅰ)求双曲线C的离心率e的取值范围；
(Ⅱ)设直线l与y轴的交点为P，且
＝
．求a的值．
答案：
解析：
解析：
|
解：(Ⅰ)由C与l相交于两个不同的点，故知方程组 有两个不同的实数解．消去y并整理得 (1－a2)x2＋2a2x－2a2＝0． ① 所以 解得0＜a＜ 双曲线的离心率 e＝ ∵0＜a＜ ∴e＞ 即离心率e的取值范围为( (Ⅱ)设A(x1，y1)，B(x2，y2)，P(0，1) ∵ ∴(x1，y1－1)＝ 由此可得x1＝ 由于x1＋x2都是方程①的根，且1－a2≠0， 所以 消去x2，得－ 由于a＞0，所以a＝ 分析：本小题主要考查直线和双曲线的概念和性质，平面向量的运算等解析几何的基本思想和综合解题能力． |
且a≠1．
＝
．
且a≠1，
且e≠
，
)∪(
，＋∞)．
＝
，
(x2，y2－1)．
x2．
x2＝－
．
x22＝－
．
＝
，
．
练习册系列答案
相关题目
－y2＝1(a＞0)与直线l：x＋y＝1相交于两个不同的点A、B．
．求a的值．
－y2＝1(a＞0)与直线l：x＋y＝1相交于两个不同的点A、B．
＝
，求a的值．
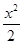－y2＝1的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q．
·
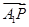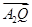＝1，求点T的坐标；
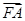＝λ·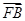
，若λ∈[－2，－1]，求|
＋
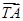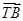|（T为（1）中的点）的取值范围．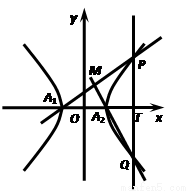
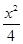－y2＝1的右焦点为F，直线l过点F且斜率为k，若直线l与双曲线C的左、右两支都相交，则直线l的斜率的取值范围是
或k≥