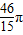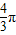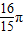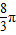题目内容
由直线x=0，x=
，y=0与曲线y=2sinx所围成的图形的面积等于（ ）
| 2π |
| 3 |
| A、3 | ||
B、
| ||
| C、1 | ||
D、
|
分析：先将围成的平面图形的面积用定积分表示出来，然后运用微积分基本定理计算定积分即可．
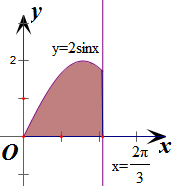
解答：解：直线x=0，x=
，y=0与曲线y=2sinx所围成的图形如右图所示，
其面积为：S=
2sinxdx=-2cosx
=-2cos
-（-2cos0）=1+2=3，
故选A．
| 2π |
| 3 |
其面积为：S=
| ∫ |
0 |
| | |
0 |
| 2π |
| 3 |
-（-2cos0）=1+2=3，故选A．
点评：本题主要考查了定积分在求面积中的应用，运用微积分基本定理计算定积分的关键是找到被积函数的原函数，属于基础题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
由直线x=0，x=2，y=0和抛物线x=
所围成的平面图形绕x轴旋转所得几何体的体积为（ ）
| 1-y |
A、
| ||
B、
| ||
C、
| ||
D、
|
由直线x=-2，x=2，y=0及曲线y=x2-x所围成的平面图形的面积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
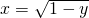所围成的平面图形绕x轴旋转所得几何体的体积为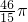
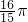
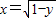所围成的平面图形绕x轴旋转所得几何体的体积为（ ）
