题目内容
由直线x=-2,x=2,y=0及曲线y=x2-x所围成的平面图形的面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据题意画出图形,如图所示,设所求的面积为S,分为三部分:第一部分:在区间-2到0上,由曲线方程的定积分;第二部分:在区间0到1上,由0减曲线方程的定积分;在区间1到2上,由曲线方程的定积分,把求出的三个定积分的值相加即为所求的面积.
解答: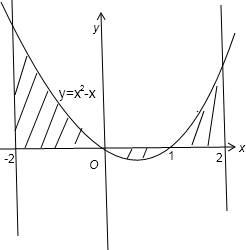 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:
设由直线x=-2,x=2,y=0及曲线y=x2-x所围成的平面图形的面积为S,
则S=∫20(x2-x)dx+∫01[0-(x2-x)]dx+∫12(x2-x)dx
=(
-
)|-20+(-
+
)|01+(
-
)|12
=
+2-
+
+
-2-
+
=
.
故选B
 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:设由直线x=-2,x=2,y=0及曲线y=x2-x所围成的平面图形的面积为S,
则S=∫20(x2-x)dx+∫01[0-(x2-x)]dx+∫12(x2-x)dx
=(
| x3 |
| 3 |
| x2 |
| 2 |
| x3 |
| 3 |
| x2 |
| 2 |
| x3 |
| 3 |
| x2 |
| 2 |
=
| 8 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 17 |
| 3 |
故选B
点评:此题考查了定积分在求面积中的应用,考查了数形结合的思想,利用定积分表示出所求的面积是解本题的关键.

练习册系列答案
相关题目
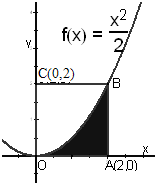 如图所示,计算图中由曲线y=
如图所示,计算图中由曲线y=


