题目内容
5.如图,直线m:3x+4y-4=0与以O1、O2、…On、…为圆心,且依次外切的半圆都相切,其中半圆O1与y轴相切,半圆圆心都在x轴的正半轴上,半径分别为r1、r2、…、rn、…,求所有半圆弧长的总和L.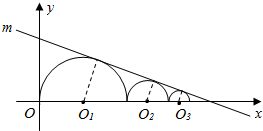
分析 由已知条件推导出{rn}是首项为$\frac{1}{2}$,公比为$\frac{1}{4}$的等比数列,由此能求出所有半圆弧长的总和.
解答 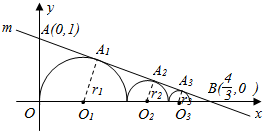 解:∵直线m:3x+4y-4=0,∴令x=0,得y=1,令y=0,得x=$\frac{4}{3}$,
解:∵直线m:3x+4y-4=0,∴令x=0,得y=1,令y=0,得x=$\frac{4}{3}$,
即OA=1,OB=$\frac{4}{3}$,∴AB=$\sqrt{{1}^{2}+(\frac{4}{3})^{2}}$=$\frac{5}{3}$,
∵∠OAB是公共角,∴∠AOB=∠O1A1B,
∴△AOB∽△O1A1B,
∴$\frac{{O}_{1}{A}_{1}}{OA}=\frac{{O}_{1}B}{AB}=\frac{OB-O{O}_{1}}{AB}$,即$\frac{{r}_{1}}{1}=\frac{\frac{4}{3}-{r}_{1}}{\frac{5}{3}}$,解得${r}_{1}=\frac{1}{2}$.
同理,$\frac{{O}_{2}{A}_{2}}{OA}=\frac{OB-O{O}_{2}}{AB}$,即$\frac{{r}_{2}}{1}=\frac{\frac{4}{3}(2{r}_{1}+{r}_{2})}{\frac{5}{3}}$,解得${r}_{2}=\frac{1}{8}$,
${r}_{3}=\frac{2-3({r}_{1}+{r}_{2})}{4}=\frac{1}{32}$,${r}_{4}=\frac{2-3({r}_{1}+{r}_{2}+{r}_{3})}{4}=\frac{1}{128}$,…
∴{rn}是首项为$\frac{1}{2}$,公比为$\frac{1}{4}$的等比数列,
∴所有半圆弧长的总和:
L=(r1+r2+…+rn)π
=[$\frac{1}{2}×\frac{1-(\frac{1}{4})^{n}}{1-\frac{1}{4}}$]π
=$\frac{2}{3}(1-\frac{1}{{4}^{n}})π$.
点评 本题考查所有半圆弧长的总和的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案| A. | -$\frac{1}{20}$ | B. | -$\frac{8}{15}$ | C. | -$\frac{27}{20}$ | D. | -$\frac{29}{15}$ |