题目内容
若已知中心在坐标原点的椭圆过点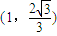 ,且它的一条准线方程为x=3,则该椭圆的方程为 .
,且它的一条准线方程为x=3,则该椭圆的方程为 .
【答案】分析:设椭圆的方程是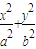 =1,由题设,中心在坐标原点的椭圆过点
=1,由题设,中心在坐标原点的椭圆过点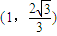 ,且它的一条准线方程为x=3,故可以得两个关于a,b,c的方程,解出参数就可得到椭圆的方程.
,且它的一条准线方程为x=3,故可以得两个关于a,b,c的方程,解出参数就可得到椭圆的方程.
解答:解:设椭圆的方程是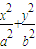 =1,
=1,
由题设,中心在坐标原点的椭圆过点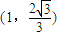 ,且它的一条准线方程为x=3,
,且它的一条准线方程为x=3,
∴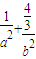 =1,
=1,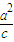 =3,又a2=c2+b2
=3,又a2=c2+b2
三式联立可以解得a=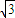 ,b=
,b=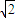 ,c=1或a=
,c=1或a=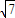 ,b=
,b=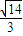 ,c=
,c=
故该椭圆的方程为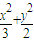 =1或
=1或 =1
=1
故应填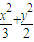 =1或
=1或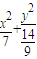 =1
=1
点评:本题考查椭圆的几何特征,利用几何特征建立三个参数a,b,c的方程,求出参数,进而求出椭圆的方程.
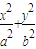 =1,由题设,中心在坐标原点的椭圆过点
=1,由题设,中心在坐标原点的椭圆过点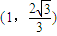 ,且它的一条准线方程为x=3,故可以得两个关于a,b,c的方程,解出参数就可得到椭圆的方程.
,且它的一条准线方程为x=3,故可以得两个关于a,b,c的方程,解出参数就可得到椭圆的方程.解答:解:设椭圆的方程是
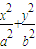 =1,
=1,由题设,中心在坐标原点的椭圆过点
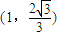 ,且它的一条准线方程为x=3,
,且它的一条准线方程为x=3,∴
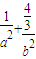 =1,
=1,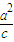 =3,又a2=c2+b2
=3,又a2=c2+b2三式联立可以解得a=
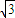 ,b=
,b=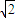 ,c=1或a=
,c=1或a=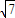 ,b=
,b=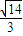 ,c=
,c=
故该椭圆的方程为
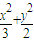 =1或
=1或 =1
=1故应填
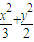 =1或
=1或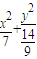 =1
=1点评:本题考查椭圆的几何特征,利用几何特征建立三个参数a,b,c的方程,求出参数,进而求出椭圆的方程.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率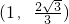 ,且它的一条准线方程为x=3,则该椭圆的方程为________.
,且它的一条准线方程为x=3,则该椭圆的方程为________.