题目内容
已知直线l:y=x,圆C1的圆心为(3,0),且经过(4,1)点.
(1)求圆C1的方程;
(2)若圆C2与圆C1关于直线l对称,点A、B分别为圆C1、C2上任意一点,求|AB|的最小值;
(3)已知直线l上一点M在第一象限,两质点P、Q同时从原点出发,点P以每秒1个单位的速度沿x轴正方向运动,点Q以每秒2
个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
(1)求圆C1的方程;
(2)若圆C2与圆C1关于直线l对称,点A、B分别为圆C1、C2上任意一点,求|AB|的最小值;
(3)已知直线l上一点M在第一象限,两质点P、Q同时从原点出发,点P以每秒1个单位的速度沿x轴正方向运动,点Q以每秒2
| 2 |
分析:(1)根据圆C1的圆心为(3,0),求得半径,从而求得圆的标准方程.
(2)求出C2的坐标,可得两圆的圆心距 C1C2 的值,再把两圆的圆心距减去这两个对称圆的半径,即得所求.
(3)设运动时间为t秒,依据题意求得PQ的坐标,可得P、Q的斜率,由点斜式求的PQ的方程.再根据当直线PQ与圆C1相切时,圆心C1到直线PQ的距离等于半径,求得t的值.
(2)求出C2的坐标,可得两圆的圆心距 C1C2 的值,再把两圆的圆心距减去这两个对称圆的半径,即得所求.
(3)设运动时间为t秒,依据题意求得PQ的坐标,可得P、Q的斜率,由点斜式求的PQ的方程.再根据当直线PQ与圆C1相切时,圆心C1到直线PQ的距离等于半径,求得t的值.
解答:解:(1)由题意可得,圆C1的圆心为(3,0),半径为
=
,
故圆C1的方程为 (x-3)2+y2=2.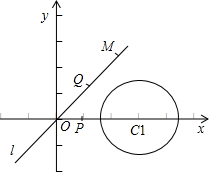
(2)若圆C2与圆C1关于直线l:y=x对称,故C2的坐标为(0,3),半径为
.
两圆的圆心距 C1C2=
=3
,故|AB|的最小值为 3
-2r=3
-2
=
.
(3)设运动时间为t秒,则由题意可得|OP|=t,|OQ|=2
t,则点P(t,0).
由于点Q在直线l:y=x上,设Q(m,n),m>0,n>0,则有 m2+n2=(2
t)2,解得 m=2t,即Q(2t,2t).
故PQ的斜率为
=2,故PQ的方程为 y-0=2(x-t),即 2x-y-2t=0.
当直线PQ与圆C1相切时,圆心C1到直线PQ的距离等于半径
,即
=
,
解得t=3±
,故当t=3±
时,直线PQ与圆C1相切.
| (4-3)2+(1-0)2 |
| 2 |
故圆C1的方程为 (x-3)2+y2=2.

(2)若圆C2与圆C1关于直线l:y=x对称,故C2的坐标为(0,3),半径为
| 2 |
两圆的圆心距 C1C2=
| 9+9 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(3)设运动时间为t秒,则由题意可得|OP|=t,|OQ|=2
| 2 |
由于点Q在直线l:y=x上,设Q(m,n),m>0,n>0,则有 m2+n2=(2
| 2 |
故PQ的斜率为
| 2t-0 |
| 2t-t |
当直线PQ与圆C1相切时,圆心C1到直线PQ的距离等于半径
| 2 |
| |2×3-0-2t| | ||
|
| 2 |
解得t=3±
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查圆的标准方程,直线和圆的位置关系,点到直线的距离公式的应用,属于中档题.

练习册系列答案
相关题目