题目内容
设函数y=f(x)的定义域为D,若对于任意x1,x2∈D且x1+x2=2a,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究并利用函数f(x)=x3-3x2-sin(πx)的对称中心,可得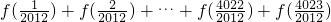 =
=
- A.4023
- B.-4023
- C.8046
- D.-8046
D
分析:函数(x)=x3-3x2-sin(πx)图象的对称中心的坐标为(1,-2),即x1+x2=2时,总有f(x1)+f(x2)=-4,再利用倒序相加,即可得到结论.
解答:由题意可知要求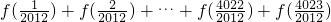 的值,
的值,
易知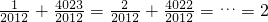 ,
,
所以函数(x)=x3-3x2-sin(πx)图象的对称中心的坐标为(1,-2),
即x1+x2=2时,总有f(x1)+f(x2)=-4
∴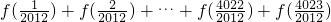 +f(
+f(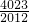 )+…+f(
)+…+f(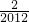 )+f(
)+f( )=-4×4023
)=-4×4023
∴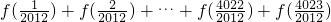 =-8046
=-8046
故选D.
点评:本题考查函数的对称性,确定函数的对称中心,利用倒序相加x1+x2=2,是解题的关键.
分析:函数(x)=x3-3x2-sin(πx)图象的对称中心的坐标为(1,-2),即x1+x2=2时,总有f(x1)+f(x2)=-4,再利用倒序相加,即可得到结论.
解答:由题意可知要求
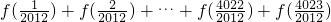 的值,
的值,易知
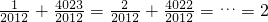 ,
,所以函数(x)=x3-3x2-sin(πx)图象的对称中心的坐标为(1,-2),
即x1+x2=2时,总有f(x1)+f(x2)=-4
∴
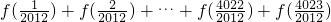 +f(
+f(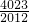 )+…+f(
)+…+f(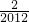 )+f(
)+f( )=-4×4023
)=-4×4023∴
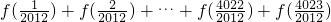 =-8046
=-8046故选D.
点评:本题考查函数的对称性,确定函数的对称中心,利用倒序相加x1+x2=2,是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目