题目内容
.(本小题满分13分)
已知函数f(x)=sinωx·cosωx-cos2ωx(ω>0)的最小正周期为.
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时f(x)的值域.
解:(Ⅰ)f(x)=sin2ωx-(cos2ωx+1)
=sin(2ωx-)-.
∵函数f(x)的周期T==,
∴ω=2.
此时f(x)的表达式为f(x)=sin(4x-)-. (6分)
(Ⅱ)由题意,得cosx=.
∵b2=ac,
∴cosx=≥=.(当且仅当a=c时等号成立)
∵0<x<π,∴0<x≤.
∴-<4x-≤π.
∴-≤sin(4x-)≤1.
∴-1≤sin(4x-)-≤.
即函数f(x)的值域为[-1,]. (13分)
=sin(2ωx-)-.
∵函数f(x)的周期T==,
∴ω=2.
此时f(x)的表达式为f(x)=sin(4x-)-. (6分)
(Ⅱ)由题意,得cosx=.
∵b2=ac,
∴cosx=≥=.(当且仅当a=c时等号成立)
∵0<x<π,∴0<x≤.
∴-<4x-≤π.
∴-≤sin(4x-)≤1.
∴-1≤sin(4x-)-≤.
即函数f(x)的值域为[-1,]. (13分)
略

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
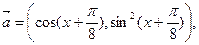
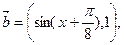 函数
函数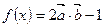
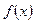 的解析式,并写出函数
的解析式,并写出函数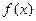 图象的对称中心坐标与对称轴方程.
图象的对称中心坐标与对称轴方程. 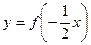 的单调递增区间;
的单调递增区间;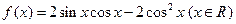 .
.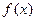 的最小正周期;
的最小正周期;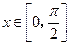 时,求函数
时,求函数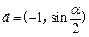 与向量
与向量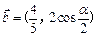 垂直,其中
垂直,其中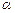 为第二象限角.
为第二象限角.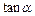 的值;
的值;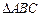 中,
中,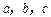 分别为
分别为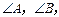
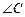 所对的边,若
所对的边,若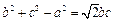 ,求
,求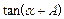 的值.
的值. 的最小正周期是
的最小正周期是



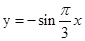 在区间
在区间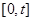 上至少取得2个最大值,则正整数t的最小值是
上至少取得2个最大值,则正整数t的最小值是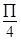 ,
,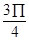 ]
]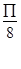 ,
,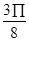 ]
]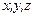 ,定义一种运算“
,定义一种运算“ ”,
”,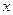
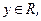
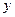
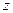 )=(
)=(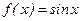
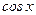 ,则
,则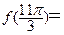
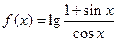 是
是  ( )
( )