题目内容
(本题满分12分)
已知向量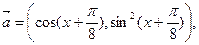
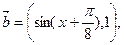 函数
函数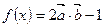
(1)求函数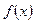 的解析式,并写出函数
的解析式,并写出函数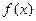 图象的对称中心坐标与对称轴方程.
图象的对称中心坐标与对称轴方程.
(2)求函数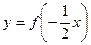 的单调递增区间;
的单调递增区间;
已知向量
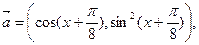
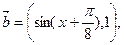 函数
函数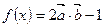
(1)求函数
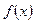 的解析式,并写出函数
的解析式,并写出函数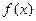 图象的对称中心坐标与对称轴方程.
图象的对称中心坐标与对称轴方程. (2)求函数
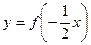 的单调递增区间;
的单调递增区间;解:(1)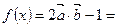
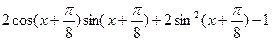
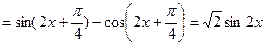 ……………..3分
……………..3分
令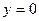 ,即
,即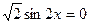 ,得
,得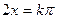 ,
,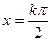 ,
,
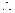 对称点为
对称点为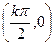 ,
,
由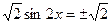 ,
, 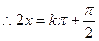 ,
,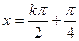 ,
,
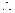 对称轴方程是直线
对称轴方程是直线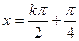 ,
, …………………………6分
…………………………6分
(2) =
=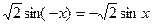 的单调递增区间
的单调递增区间
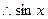 递减
递减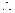
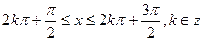
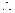
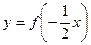 的单调递增区间是
的单调递增区间是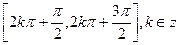 …………12分
…………12分
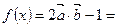
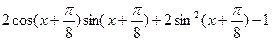
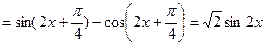 ……………..3分
……………..3分令
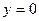 ,即
,即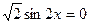 ,得
,得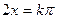 ,
,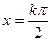 ,
,
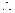 对称点为
对称点为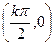 ,
,
由
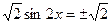 ,
, 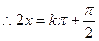 ,
,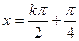 ,
,
 对称轴方程是直线
对称轴方程是直线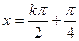 ,
, …………………………6分
…………………………6分(2)
 =
=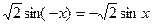 的单调递增区间
的单调递增区间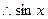 递减
递减
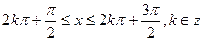
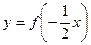 的单调递增区间是
的单调递增区间是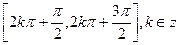 …………12分
…………12分略

练习册系列答案
相关题目
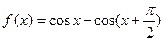 ,
,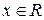 .
.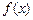 的最大值;
的最大值;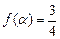 ,求
,求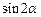 的值.
的值.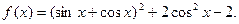
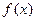 的最小正周期T;
的最小正周期T; 时,求函数
时,求函数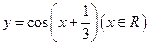 的图像上所有的点( )
的图像上所有的点( )
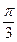 个单位长度 B 向右平行移动
个单位长度 B 向右平行移动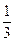 个单位长度 D 向右平行移
个单位长度 D 向右平行移 动
动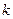
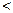
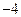 ,则函数
,则函数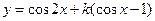 的最小值是(
的最小值是(  )
)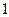
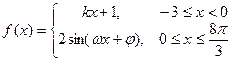 的图象如图,则( )
的图象如图,则( )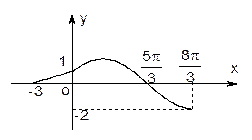
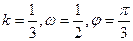
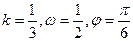
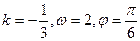
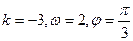
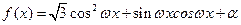 (其中
(其中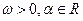 ),且
),且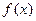 的图象在
的图象在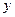 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为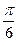 。
。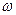 的值。
的值。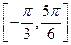 上的最小值为
上的最小值为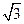 ,求
,求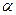 的值。
的值。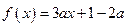 在
在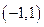 内存在
内存在 使
使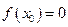 ,则
,则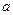 的取值范围是
的取值范围是