题目内容
19.已知无穷等比数列{an}中,a1=1,公比为q(q>0),Sn是数列的前n项的和,记Tn=a2+a4+a6+…+a2n,求$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{T}_{n}}$的值.分析 对q分类讨论,利用等比数列的前n项和公式可得Sn,Tn,再利用数列极限法则即可得出.
解答 解:当q=1时,Sn=n,Tn=n,∴$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{T}_{n}}$=$\underset{lim}{n→∞}\frac{n}{n}$=1.
当q≠1时,Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,Tn=$\frac{{a}_{1}q(1-{q}^{2n})}{1-{q}^{2}}$,∴$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{T}_{n}}$=$\underset{lim}{n→∞}$$\frac{1+q}{q(1+{q}^{n})}$.
当0<q<1时,$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{T}_{n}}$=$\frac{1+q}{q}$.
当1<q时,$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{T}_{n}}$=0.
综上可得:$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{T}_{n}}$=$\left\{\begin{array}{l}{1,q=1}\\{\frac{1+q}{q},0<q<1}\\{0,q>1}\end{array}\right.$.
点评 本题考查了等比数列的通项公式与前n项和公式、数列极限运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.若数列an=$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$,则a5-a4=( )
| A. | $\frac{1}{10}$ | B. | -$\frac{1}{10}$ | C. | $\frac{1}{90}$ | D. | -$\frac{19}{90}$ |
8.设x、y∈R,则命题“x2+y2>1”是命题“|x|+|y|>1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
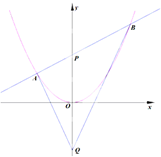 如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.
如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.