题目内容
(本小题满分12分)
设函数 ,其中
,其中 是某范围内的随机数,分别在下列条件下,求事件A “
是某范围内的随机数,分别在下列条件下,求事件A “ 且
且 ”发生的概率.
”发生的概率.
(Ⅰ)若随机数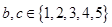 ;
;
(Ⅱ)已知随机函数 产生的随机数的范围为
产生的随机数的范围为 ,
,  是算法语句
是算法语句 和
和 的执行结果.(注: 符号“
的执行结果.(注: 符号“ ”表示“乘号”)
”表示“乘号”)
【答案】
(Ⅰ)事件A发生的概率为 (Ⅱ)事件
(Ⅱ)事件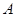 的发生概率为
的发生概率为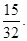
【解析】本试题主要是考查了古典概型和几何概型概率的运用。
(1)它是个古典概型,根据条件得到试验的基本事件空间,然后分析得到事件A包含的基本事件数,利用概率公式求解得到。
(2)它是个几何概型的模型,先分析基本事件空间是表示的那个面积,然后研究事件发生的面积,利用面积比来求解概率值。
解:由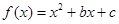 知,事件A “
知,事件A “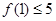 且
且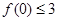 ”,即
”,即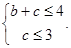 1分
1分
(Ⅰ)因为随机数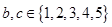 ,所以共等可能地产生
,所以共等可能地产生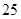 个数对
个数对 ,
,
列举如下: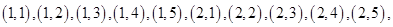

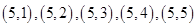 …………4分
…………4分
事件A :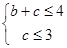 包含了其中
包含了其中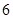 个数对
个数对 ,即:
,即:
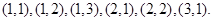 ····················· 6分
····················· 6分
所以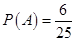 ,即事件A发生的概率为
,即事件A发生的概率为 ················· 7分
················· 7分
(Ⅱ)由题意,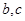 均是区间
均是区间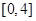 中的随机数,产生的点
中的随机数,产生的点 均匀地分布在边长为4的正方形区域
均匀地分布在边长为4的正方形区域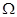 中(如图),其面积
中(如图),其面积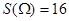 . ······························· 8分
. ······························· 8分
事件A :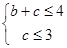 所对应的区域为如图所示的梯形(阴影部分),
所对应的区域为如图所示的梯形(阴影部分),

其面积为: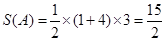 .
…………10分
.
…………10分
所以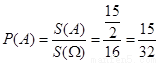 ,即事件
,即事件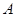 的发生概率为
的发生概率为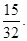 12分
12分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目