题目内容
设平面区域D是由双曲线x2-
=1的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部.当(x,y)∈D时,2x+y的最大值为( )
| y2 |
| 4 |
| A、8 | B、0 | C、-2 | D、16 |
分析:由题意平面区域D是由双曲线 x2-
=1的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以先由题意找到平面区域D,对于目标函数2x+y的最大值可以利用角点法进行求解.
| y2 |
| 4 |
解答:解:有平面区域D是由双曲线 x2-
=1的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以得到区域为:
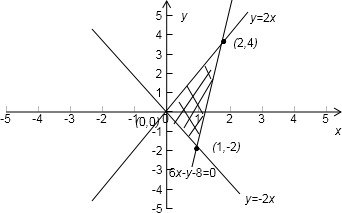
由于目标函数为2x+y,三角形的三个顶点坐标为(0,0),(1,-2),(2,4).
所求目标函数为2x+y的最大值为2×2+4=8
故选A
| y2 |
| 4 |

由于目标函数为2x+y,三角形的三个顶点坐标为(0,0),(1,-2),(2,4).
所求目标函数为2x+y的最大值为2×2+4=8
故选A
点评:此题考查了双曲线的渐进性方程,线性规划求最值时目标函数的几何含义及学生用图的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目