题目内容
对于以下命题
①若(
)a=(
)b,则a>b>0;
②设a,b,c,d是实数,若a2+b2=c2+d2=1,则abcd的最小值为-
;
③若x>0,则((2-x)ex<x+2;
④若定义域为R的函数y=f(x),满足f(x)+f(x+2)=2,则其图象关于点(2,1)对称.
其中正确命题的序号是 (写出所有正确命题的序号).
①若(
| 1 |
| 2 |
| 1 |
| 3 |
②设a,b,c,d是实数,若a2+b2=c2+d2=1,则abcd的最小值为-
| 1 |
| 4 |
③若x>0,则((2-x)ex<x+2;
④若定义域为R的函数y=f(x),满足f(x)+f(x+2)=2,则其图象关于点(2,1)对称.
其中正确命题的序号是
分析:根据函数的性质分别进行判断即可.
解答: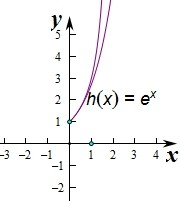 解:①当a=b=0时.满足(
解:①当a=b=0时.满足(
)a=(
)b=1,但a>b>0不成立,∴①错误.
②设a,b,c,d是实数,若a2+b2=c2+d2=1,
则a2+b2≥2|ab|,c2+d2=≥2|cd|,
∴|ab|≤
,|cd|≤
,
∴|abcd|=|ab|•|cd|≤
•
=
,
∴-
≤abcd≤
,
则abcd的最小值为-
,∴②正确.
③若x=2,则不等式等价为0<4成立,
若x>2时,2-x<0,x+2>4,∴不等式成立.
若0<x<2,则不等式等价为ex<
=-1-
;由图象可知不等式成立.
故③正确.
④若定义域为R的函数y=f(x),满足f(x)+f(x+2)=2,则f(x+2)+f(x+4)=2,即f(x+2)+f(x+4)=f(x+2)+f(x),
∴f(x+4)=f(x),即函数的周期是4,则其图象关于点(2,1)对称不正确.
其中正确命题的序号是②③,
故答案为:②③.
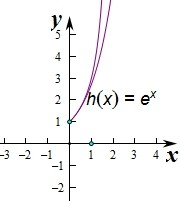 解:①当a=b=0时.满足(
解:①当a=b=0时.满足(| 1 |
| 2 |
| 1 |
| 3 |
②设a,b,c,d是实数,若a2+b2=c2+d2=1,
则a2+b2≥2|ab|,c2+d2=≥2|cd|,
∴|ab|≤
| 1 |
| 2 |
| 1 |
| 2 |
∴|abcd|=|ab|•|cd|≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴-
| 1 |
| 4 |
| 1 |
| 4 |
则abcd的最小值为-
| 1 |
| 4 |
③若x=2,则不等式等价为0<4成立,
若x>2时,2-x<0,x+2>4,∴不等式成立.
若0<x<2,则不等式等价为ex<
| x+2 |
| 2-x |
| 4 |
| x-4 |
故③正确.
④若定义域为R的函数y=f(x),满足f(x)+f(x+2)=2,则f(x+2)+f(x+4)=2,即f(x+2)+f(x+4)=f(x+2)+f(x),
∴f(x+4)=f(x),即函数的周期是4,则其图象关于点(2,1)对称不正确.
其中正确命题的序号是②③,
故答案为:②③.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
 =
= ,则a>b>0;
,则a>b>0; ;
;