题目内容
(本小题满分12分)
已知函数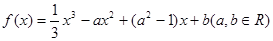 ,
,
(1)若 为
为 的极值点,求
的极值点,求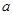 的值;
的值;
(2)若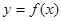 的图象在点(1,
的图象在点(1, )处的切线方程为
)处的切线方程为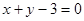 ,求
,求 在区间[-2, 4]上的最大值。
在区间[-2, 4]上的最大值。
(3)当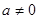 时,若
时,若 在区间(-1,1)上不单调,求
在区间(-1,1)上不单调,求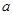 的取值范围。
的取值范围。
【答案】
(1) 或2.
或2.
(2) 在区间
在区间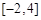 上的最大值为8.
上的最大值为8.
(3)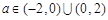 .
.
【解析】解:⑴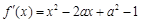 ∵
∵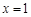 是
是 的极值点,
的极值点,
∴ ,即
,即 ,解得
,解得 或2.
…………3分
或2.
…………3分
⑵∵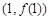 在
在 上.∴
上.∴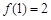 ∵
∵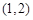 在
在 上,
上,
∴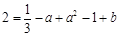 又
又 ,∴
,∴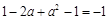 ∴
∴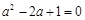 ,
,
解得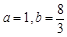 ∴
∴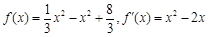
由 可知
可知 和
和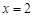 是极值点.∵
是极值点.∵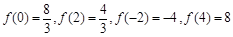
∴ 在区间
在区间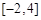 上的最大值为8. …………8分
上的最大值为8. …………8分
⑶因为函数 在区间
在区间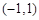 不单调,所以函数
不单调,所以函数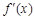 在
在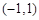 上存在零点.
上存在零点.
而 的两根为
的两根为 ,
,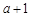 ,区间长为
,区间长为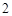 ,
,
∴在区间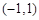 上不可能有2个零点.
上不可能有2个零点.
所以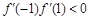 ,∵
,∵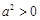 ,∴
,∴ .
.
又∵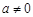 ,∴
,∴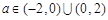 .
…………12分
.
…………12分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目