题目内容
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)证明见;解析;定点
;(2)证明见;解析;定点![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据直线与圆相切得圆心到直线距离等于半径列一个方程,再根据等边三角形性质得![]() ,解方程组得
,解方程组得![]() ,即得结果;
,即得结果;
(2)先设直线方程,与椭圆方程联立分别解得M,N坐标,再求斜率(注意讨论),利用点斜式得直线方程,即得定点坐标;
(3)利用韦达定理以及弦长公式得![]() ,再根据三角形面积公式得
,再根据三角形面积公式得![]() 面积的函数关系式,最后根据基本不等式求最大值.
面积的函数关系式,最后根据基本不等式求最大值.
(1)由题意可得: ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]() .
.
(2)由题意知![]() ,设:
,设:![]() ,
,![]() .
.
由 消去
消去![]() 得:
得:![]() ,
,
解得:![]() 或
或![]() (舍去),
(舍去),![]() ,
,
 ,同理可得:
,同理可得: .
.
i:当![]() 时,直线
时,直线![]() 斜率存在,
斜率存在,
 ,
,
![]() ,
,![]() 直线
直线![]() 过定点
过定点![]() .
.
ii:当![]() 时,直线
时,直线![]() 斜率不存在,直线方程为:
斜率不存在,直线方程为:![]() ,也过定点
,也过定点![]() ,
,
综上所述:直线![]() 过定点
过定点![]() .
.
(3)设![]() ,由(2)知:
,由(2)知:

 ,
,
令![]() ,
, 在
在![]() 单调递减,
单调递减,
![]() ∴当
∴当![]() 时,
时, .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
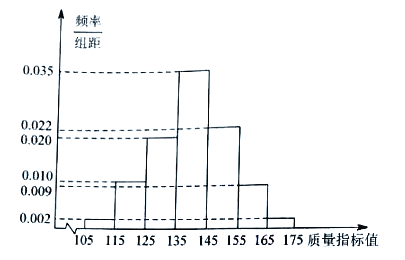
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:

(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: ,
,![]() (回归方程
(回归方程![]() 中)
中)
【题目】《最强大脑》是江苏卫视引进德国节目《Super Brain》而推出的大型科学竞技真人秀节目,节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试,![]() 分以上才有机会入围,某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各
分以上才有机会入围,某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各![]() 名,然后对这
名,然后对这![]() 名学生进行脑力测试,规定:分数不小于
名学生进行脑力测试,规定:分数不小于![]() 分为“入围学生”,分数小于
分为“入围学生”,分数小于![]() 分为“未入围学生”,已知男生入围
分为“未入围学生”,已知男生入围![]() 人,女生未入围
人,女生未入围![]() 人,
人,
(1)根据题意,填写下面的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关.
以上的把握认为脑力测试后是否为“入围学生”与性别有关.
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | ||
女生 | 80 | ||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取![]() 名学生.
名学生.
(ⅰ)求这![]() 名学生中女生的人数;
名学生中女生的人数;
(ⅱ)若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),求这![]() 名学生中女生测试分数的平均分的最小值.
名学生中女生测试分数的平均分的最小值.
附:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |