题目内容
（2013•长春一模）请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．如图，已知⊙O和⊙M相交于A、B两点，AD为⊙M的直径，直线BD交⊙O于点C，点G为
 |
| BD |
（1）求证：AG•EF=CE•GD；
（2）求证：
| GF |
| AG |
| EF2 |
| CE2 |
分析：（1）连接AB，由圆周角定理，及G为
中点，可得∠GAD=∠FCE，∠CEF=∠ABC=90°，进而得到△CEF∽△AGD，根据相似三角形对应边成比例，可得AG•EF=CE•GD；
（2）由（1）可得∠DFG=∠CFE=∠ADG，故△AGD∽△DGF，根据相似三角形对应边成比例，可得
=
=
，进而
=
．
|
| BD |
（2）由（1）可得∠DFG=∠CFE=∠ADG，故△AGD∽△DGF，根据相似三角形对应边成比例，可得
| GF |
| DG |
| DG |
| AG |
| EF |
| CE |
| GF |
| AG |
| EF2 |
| CE2 |
解答：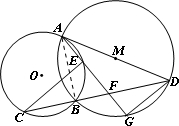
证明（1）：已知AD为⊙M的直径，连接AB，
则∠BCE=∠BAE，∠CEF=∠ABC=90°，
由点G为弧BD的中点可知∠GAD=∠BAE=∠FCE，
故△CEF∽△AGD，所以有
=
，
即AG•EF=CE•GD．（5分）
（2）由（1）知∠DFG=∠CFE=∠ADG，
故△AGD∽△DGF，
所以
=
=
，
即
=
．（10分）
证明（1）：已知AD为⊙M的直径，连接AB，则∠BCE=∠BAE，∠CEF=∠ABC=90°，
由点G为弧BD的中点可知∠GAD=∠BAE=∠FCE，
故△CEF∽△AGD，所以有
| CE |
| AG |
| EF |
| GD |
即AG•EF=CE•GD．（5分）
（2）由（1）知∠DFG=∠CFE=∠ADG，
故△AGD∽△DGF，
所以
| GF |
| DG |
| DG |
| AG |
| EF |
| CE |
即
| GF |
| AG |
| EF2 |
| CE2 |
点评：本小题主要考查平面几何中三角形相似的判定与性质，以及圆中角的性质等知识．
练习册系列答案
相关题目