题目内容
 (2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.
(2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.(1)求证:在四棱锥S-ABCD中AB⊥SD.
(2)若AC长等于6,求异面直线AB与SC之间的距离.
分析:法一:(立体几何法)(1)由题设条件将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC可以判断棱锥是一个正四面体,由正四面体的性质再结合三垂线定理可证明结论;
(2)由题设条件,可将求异面直线AB与SC之间的距离的问题转化为求直线AB与平面SCD之间的距离,进而转化为点到面的距离即可求得两异面直线间的距离.
法二:(向量法)作SO⊥平面ABCD于O,取BA的三等分点E,则OE,OC,OS两两互相垂直建立坐标系,给出各点的空间坐标
(1)求出两直线AB与SD的方向向量,利用数量积为0与两向量垂直的关系证明两直线垂直即可;
(2)可两异面直线公垂线的方向向量的坐标为
=(x,y,z),再由
建立方程求出此向量的坐标,然后由公式d=
求出AS在此方向上的投影即可得到两异面直线之间的距离.
(2)由题设条件,可将求异面直线AB与SC之间的距离的问题转化为求直线AB与平面SCD之间的距离,进而转化为点到面的距离即可求得两异面直线间的距离.
法二:(向量法)作SO⊥平面ABCD于O,取BA的三等分点E,则OE,OC,OS两两互相垂直建立坐标系,给出各点的空间坐标
(1)求出两直线AB与SD的方向向量,利用数量积为0与两向量垂直的关系证明两直线垂直即可;
(2)可两异面直线公垂线的方向向量的坐标为
| n |
|
|
| ||||
|
|
解答:解法一:(1)易知S-ABD是正四面体,作SO⊥平面ABCD于O,则O是正三角形ABD的垂心
∵AB⊥OD
∴AB⊥SD(三垂线定理)
(2)∵AC=6∴CD=SD=2
,设B到平面SCD的距离为d,SO=
=2
于是
•(2
)2•2
=
•(2
)2•d⇒d=
又AB∥平面SCD
∴异面直线AB与SC之间的距离即为点B到平面SCD的距离d,
所以两异面直线之间的距离为
.
解法二:作SO⊥平面ABCD于O,取BA的三等分点E,则OE,OC,OS两两互相垂直建立坐标系(如图)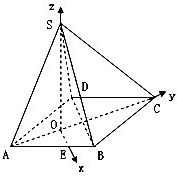
A(-2,0,0,) B(1,
,0)D(1,-
,0)
S(0,0,2
)
=(3,
,0)
=(1,-
,-2
)
(1)∵
•
=3×1+
×(-
)+0×(-2
)=0
∴AB⊥SD
(2)又C(4,0,0),可得
=(4,0,-2
),设
=(x,y,z)是两异面直线公垂线的方向向量,
于是有
代入向量坐标,令x=1,得
∴
=(1,-
,
),又
=(2,0,2
)
∴两异面直线之间的距离d=
=
=
∵AB⊥OD
∴AB⊥SD(三垂线定理)
(2)∵AC=6∴CD=SD=2
| 3 |
| SA2-AO2 |
| 2 |
于是
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 6 |
又AB∥平面SCD
∴异面直线AB与SC之间的距离即为点B到平面SCD的距离d,
所以两异面直线之间的距离为
| 6 |
解法二:作SO⊥平面ABCD于O,取BA的三等分点E,则OE,OC,OS两两互相垂直建立坐标系(如图)

A(-2,0,0,) B(1,
| 3 |
| 3 |
S(0,0,2
| 2 |
| AB |
| 3 |
| SD |
| 3 |
| 2 |
(1)∵
| AB |
| SD |
| 3 |
| 3 |
| 2 |
∴AB⊥SD
(2)又C(4,0,0),可得
| SC |
| 2 |
| n |
于是有
|
|
∴
| n |
| 3 |
| 2 |
| AS |
| 2 |
∴两异面直线之间的距离d=
|
| ||||
|
|
| 2+4 | ||
|
| 6 |
点评:本题考查求两异面直线之间的距离及两线的垂直关系的判定,本解答给出两种解法,一个是传统方法几何法,一个是空间向量法,学习时要注意对比、体会两种方法的不同与特征,体会向量法求解立体几何题的过程与特点.本题考查了数形结合的思想与转化的思想.

练习册系列答案
相关题目