题目内容
15. 在平行四边形ABCD中,∠A=60°,AB=2,AD=4,点E,F分别为边AD,BC的中点,将△ABE沿BE边折起,形成四棱锥A′-BCDE.如图所示.
在平行四边形ABCD中,∠A=60°,AB=2,AD=4,点E,F分别为边AD,BC的中点,将△ABE沿BE边折起,形成四棱锥A′-BCDE.如图所示.(1)当∠A′BC的余弦值为何值时,平面A′BE⊥平面BCDE?
(2)当G为A′D的中点时,求证:A′F∥平面EGC;
(3)在(1)的前提下,求二面角A′-DE-B的正切值.
分析 (1)如图所示,取BE的中点O,连接FO,A′O,EF.由已知可得:四边形ABFE是菱形.可得OF⊥BE,A′O⊥BE.要满足平面A′BE⊥平面BCDE,则必有A′O⊥OF.在△A′BF中,由余弦定理可得:cos∠A′BF=$\frac{{A}^{′}{B}^{2}+B{F}^{2}-{A}^{′}{F}^{2}}{2{A}^{′}B•BF}$即可得出.
(2)连接A′A,AF.由四边形AFCE是平行四边形,可得AF∥EC,得到AF∥平面EGC.利用三角形中位线定理可得:AA′∥EG,同理可得AA′∥平面EGC,从而得到平面AA′F∥平面EGC,即可证明A′F∥平面EGC;
(3)在(1)的前提下,可得A′O⊥平面BCDE,则∠ODA′是二面角A′-DE-B的平面角.在△ODE中,由余弦定理可得:OD.利用tan∠ODA′=$\frac{{A}^{′}O}{OD}$即可得出.
解答 (1)解:如图所示,取BE的中点O,连接FO,A′O,EF.
由已知可得:四边形ABFE是菱形.
∴OF⊥BE,A′O⊥BE.
要满足平面A′BE⊥平面BCDE,则必有A′O⊥OF.
∴${A}^{′}F=\sqrt{2}OF$=$\sqrt{6}$.
在△A′BF中,由余弦定理可得:cos∠A′BF=$\frac{{A}^{′}{B}^{2}+B{F}^{2}-{A}^{′}{F}^{2}}{2{A}^{′}B•BF}$=$\frac{1}{4}$.
因此当∠A′BC的余弦值=$\frac{1}{4}$时,平面A′BE⊥平面BCDE.
(2)证明:连接A′A,AF.
由四边形AFCE是平行四边形,∴AF∥EC,
又AF?平面EGC,EC?平面EGC,
∴AF∥平面EGC.
由G,E分别为线段A′D,AD的中点,
∴AA′∥EG,同理可得AA′∥平面EGC.
又A′A∩AF=A,
∴平面AA′F∥平面EGC,
∴A′F∥平面EGC;
(3)解:在(1)的前提下,
A′O⊥平面BCDE,连接OD.
则∠ODA′是二面角A′-DE-B的平面角.
在△ODE中,由余弦定理可得:OD2=OE2+ED2-2OE•EDcos∠OED=1+22-2×1×2cos120°=7,
∴OD=$\sqrt{7}$.
∴tan∠ODA′=$\frac{{A}^{′}O}{OD}$=$\frac{\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$.
点评 本题考查了线面面面垂直与平行的判定与性质定理、三角形中位线定理及平行四边形菱形判定与性质、等边三角形与直角三角形的性质、二面角的平面角,考查了空间想象能力、推理能力与计算能力,属于中档题.

| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 25 | 0.050 |
| 第2组 | [165,170) | 175 | 0.350 |
| 第3组 | [170,175) | 150 | |
| 第4组 | [175,180) | 0.200 | |
| 第5组 | [180,185) | 50 | 0.100 |
| 合计 | 500 | 1000 | |
(2)在(1)的前提下,政府的3个下属机关决定先后用相同的方式在12名考生中随机抽取2名考生接受考官的面试,记抽取到第5组的A考生面试的下属机关的个数为x,求的分布列和期望.
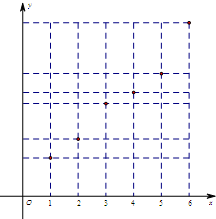 某地区在六年内第x年的生产总值y(单位:亿元)与x之间的关系如图所示,则下列四个时段中,生产总值的年平均增长率最高的是( )
某地区在六年内第x年的生产总值y(单位:亿元)与x之间的关系如图所示,则下列四个时段中,生产总值的年平均增长率最高的是( )| A. | 第一年到第三年 | B. | 第二年到第四年 | C. | 第三年到第五年 | D. | 第四年到第六年 |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
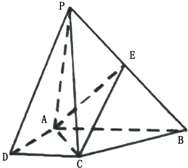 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥平面PCD,PA⊥CB,AB=2AD=2CD=2,E为PB的中点
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥平面PCD,PA⊥CB,AB=2AD=2CD=2,E为PB的中点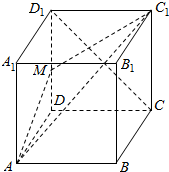 如图M是棱长为2的正方体ABCD-A1B1C1D1的棱DD1的中点.
如图M是棱长为2的正方体ABCD-A1B1C1D1的棱DD1的中点.