题目内容
5.已知函数f(x)=lnx+$\frac{a}{x}$(x>0).(1)当a=2时,求函数f(x)的单调区间;
(2)若f(x)在[1,e]上的最小值为2,求a的值.
分析 (1)把a=2代入函数解析式,求导后得到导函数的零点,由导函数的零点对定义域分段,根据导函数在各区间段内的符号求得原函数的单调期间;
(2)对原函数求导,然后分a≤0,0<a≤1,1<a<e,a≥e四种情况讨论原函数在[1,e]上的单调性,并求得最小值,由最小值等于2求得a的值.
解答 解:(1)当a=2时,$f(x)=lnx+\frac{2}{x}$,${f}^{′}(x)=\frac{1}{x}-\frac{2}{{x}^{2}}=\frac{x-2}{{x}^{2}}$.
当0<x<2时,f′(x)<0,当x>2时,f′(x)>0.
∴f(x)的减区间为(0,2);增区间为(2,+∞);
(2)由f(x)=lnx+$\frac{a}{x}$(x>0),得${f}^{′}(x)=\frac{1}{x}-\frac{a}{{x}^{2}}=\frac{x-a}{{x}^{2}}$,
若a≤0,则f′(x)≥0,函数f(x)在[1,e]上为增函数,
f(x)min=f(1)=a,则a=2,不合题意;
若a>0,则当0<a≤1时,在[1,e]上,f′(x)≥0,函数f(x)在[1,e]上为增函数,
f(x)min=f(1)=a,则a=2,不合题意;
当1<a<e时,在(0,a)上,f′(x)<0,f(x)为减函数,在(a,e)上,f′(x)>0,f(x)为增函数.
∴f(x)min=f(a)=lna+1,由lna+1=2,解得:a=e,不合题意;
当a≥e时,在[1,e]上,f′(x)≤0,f(x)在[1,e]上为减函数,
$f(x)_{min}=f(e)=1+\frac{a}{e}$,由$1+\frac{a}{e}=2$,解得a=e.
综上,a=e.
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数的最值,着重考查分类讨论的数学思想方法,是中高档题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案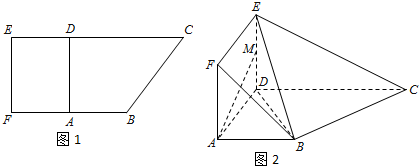
 如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.
如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.
 在平行四边形ABCD中,∠A=60°,AB=2,AD=4,点E,F分别为边AD,BC的中点,将△ABE沿BE边折起,形成四棱锥A′-BCDE.如图所示.
在平行四边形ABCD中,∠A=60°,AB=2,AD=4,点E,F分别为边AD,BC的中点,将△ABE沿BE边折起,形成四棱锥A′-BCDE.如图所示.