题目内容
已知a∈R,函数f(x)=x2|x-a|.(1)当a=2时,求使f(x)=x成立的x的集合;
(2)求函数y=f(x)在区间[1,2]上的最小值.
解:(1)由题意,f(x)=x2|x-2|.
当x<2时,f(x)=x2(2-x)=x,解得x=0或x=1;
当x≥2时,f(x)=x2(x-2)=x,解得x=1+![]() .
.
综上,所求解集为{0,1,1+![]() }.
}.
(2)设此最小值为m.
①当1<a≤1时,在区间[1,2]上,f(x)=x3-ax2.
因为f′(x)=3x2-2ax=3x(x-![]() a)>0,x∈(1,2),
a)>0,x∈(1,2),
则f(x)是区间[1,2]上的增函数,所以m=f(1)=1-a.
②当1<a≤2时,在区间[1,2]上,f(x)=x2|x-a|≥0,由f(a)=0知m=f(a)=0.
③当a>2时,在区间[1,2]上,f(x)=ax2-x3.f′(x)=2ax-3x2=3x(![]() a-x).
a-x).
若a≥3,在区间(1,2)内f′(x)>0,从而f(x)为区间[1,2]上的增函数,由此得m=f(1)=a-1.
若2<a<3,则1<![]() a<2.
a<2.
当1<x<![]() a时,f′(x)>0,从而f(x)为区间[1,
a时,f′(x)>0,从而f(x)为区间[1,![]() a]上的增函数;
a]上的增函数;
当![]() a<x<2时,f′(x)<0,从而f(x)为区间[
a<x<2时,f′(x)<0,从而f(x)为区间[![]() a,2]上的减函数.
a,2]上的减函数.
因此,当2<a<3时,m=f(1)=a-1或m=f(2)=4(a-2).
当2<a≤![]() 时,4(a-2)≤a-1,故m=4(a-2);
时,4(a-2)≤a-1,故m=4(a-2);
当![]() <a<3时,a-1<4(a-2),故m=a-1.
<a<3时,a-1<4(a-2),故m=a-1.
综上所述,所求函数的最小值m=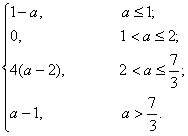

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目