题目内容
已知等比数列![]() 的各项均为不等于1的正数,数列
的各项均为不等于1的正数,数列![]() 满足ynlogxna=2,(a>0且a¹1),设y3=18,y6=12,则
满足ynlogxna=2,(a>0且a¹1),设y3=18,y6=12,则
(1)数列![]() 前多少项和最大?最大值为多少;
前多少项和最大?最大值为多少;
(2)试判断是否存在自然数M,使得n>M时xn>1恒成立,若存在,求出相应的M,若不存在,请说明理由;
(3)an=logxnxn+1(n¹12)的单调性如何?
答案:
解析:
解析:
解:(1)∵ xn¹1且xn>0 ∴ ∴ (2)由(1)可知,24-2n=2logaxnÞxn=a12-n(a>0且a¹1) 若xn>1,则a12-n>1,当a>1时,n<12,与n>M时恒成立矛盾,故不存在,当0<a<1时,n>12,所以存在M=12,13,…,当n>M时xn>1恒成立. (3) |

练习册系列答案
相关题目
 的各项均为正数,公比
的各项均为正数,公比 ,设
,设 ,
, ,则
,则 与
与 的大小关系是
的大小关系是  B.
B. C.
C. D.无法确定
D.无法确定 ,定义数列
,定义数列 为数列
为数列 =2,
=2,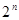 ,则数列
,则数列 =
=  ,
, ,则
,则 =
=
 的各项均为正数,且
的各项均为正数,且 .
. ,求数列
,求数列 的前n项和.
的前n项和. ,求数列{
,求数列{ }的前
}的前 项和.
项和. 的各项均为正数,且
的各项均为正数,且
 ,求数列
,求数列 的前n项和
的前n项和