题目内容
(14分)已知等比数列![]() 的各项均为正数,且公比不等于1,数列
的各项均为正数,且公比不等于1,数列![]() 对任意正整数n,均有:
对任意正整数n,均有:![]()
成立,又![]() 。
。
(Ⅰ)求数列![]() 的通项公式及前n项和
的通项公式及前n项和![]() ;
;
(Ⅱ)在数列![]() 中依次取出第1项,第2项,第4项,第8项,……,第
中依次取出第1项,第2项,第4项,第8项,……,第![]() 项,……,组成一个新数列
项,……,组成一个新数列![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(Ⅲ)当![]() 时,比较
时,比较![]() 与
与![]() 的大小。
的大小。
解析:(I)设公比为![]() ……………………2分
……………………2分
代入![]()
得
![]()
即![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() 是等差数列 ……………………4分
是等差数列 ……………………4分
![]() =2 ∴
=2 ∴![]() …………6分
…………6分
(Ⅱ)![]()
![]()
![]()
![]() ……………………8分
……………………8分
(3)![]()
![]() 时,
时,![]() 时,
时,![]()
猜测![]() 时,
时,![]() ……………………10分
……………………10分
用数学归纳法证明如下
(1)![]() 时,
时,![]() (已证)
(已证)
(2)假设![]() 时不等式成立,即
时不等式成立,即![]() ……………………12分
……………………12分
![]() 时,
时,![]()
又![]()
∴![]()
即![]() 时,不等式成立。
时,不等式成立。
由(1)(2)知,当![]() 时,
时,![]() ……………14分
……………14分

练习册系列答案
相关题目
 的各项均为正数,公比
的各项均为正数,公比 ,设
,设 ,
, ,则
,则 与
与 的大小关系是
的大小关系是  B.
B. C.
C. D.无法确定
D.无法确定 ,定义数列
,定义数列 为数列
为数列 =2,
=2,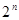 ,则数列
,则数列 =
=  ,
, ,则
,则 =
=
 的各项均为正数,且
的各项均为正数,且 .
. ,求数列
,求数列 的前n项和.
的前n项和. ,求数列{
,求数列{ }的前
}的前 项和.
项和. 的各项均为正数,且
的各项均为正数,且
 ,求数列
,求数列 的前n项和
的前n项和