题目内容
7.设函数f(x)=|x2-2x-1|,若a>b>1且f(a)=f(b),则ab-a-b的取值范围是(-1,1).分析 作出函数f(x)的图象,由a>b>1,且f(a)=f(b)可得 (a-1)2+(b-1)2=4.设a-1=2cosθ,b-1=2sinθ,θ∈(0,π4π4),根据ab-a-b=2sin2θ-1,利用正弦函数的定义域和值域求得ab-a-b的范围.
解答 解:作出函数f(x)的图象,如图: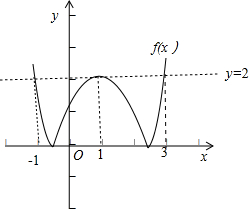
可得f(x)=|x2-2x-1|的图象关于直线x=1对称,
且f(1-√2√2)=f(1+√2√2)=0,
f(3)=f(-1)=f(1)=2,
由a>b>1,且f(a)=f(b),得a2-2a-1=-(b2-2b-1),整理得 (a-1)2+(b-1)2=4.
设a-1=2cosθ,b-1=2sinθ,θ∈(0,π4π4),
则ab-a-b=(a-1)(b-1)-1=2sin2θ-1,
由sin2θ∈(0,1),可得2sin2θ-1∈(-1,1),即ab-a-b∈(-1,1),
即:-1<ab-a-b<1.
故答案为:(-1,1).
点评 本题主要考查了二次函数的性质,同时考查了分析问题的能力,计算能力,讨论的数学思想,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
18.在△ABC中,角A、B、C的对边分别是a,b,c,若a=2,b=2√2√2,且三角形有两解,则角A的取值范围是( )
| A. | (0,π4π4) | B. | (π4π4,π2π2) | C. | (π4π4,3π43π4) | D. | (π4π4,π3π3) |
19.已知命题p:“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,命题q:“a1212>b12>b12”的充要条件为“lna>lnb”,则下列复合命题中假命题是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨¬q | D. | p∧(¬q) |
 如图,在直四棱柱ABCD-A1B1C1D1中,AD∥BC,E是DD1的中点,F是平面B1C1E与直线AA1的交点.证明:EF∥A1D1.
如图,在直四棱柱ABCD-A1B1C1D1中,AD∥BC,E是DD1的中点,F是平面B1C1E与直线AA1的交点.证明:EF∥A1D1.