题目内容
已知复数z是方程x2+2x+2=0的解,且 Imz>0,若| a |
| z |
. |
| z |
分析:由题意,复数z是方程x2+2x+2=0的解,且 Imz>0,由此方程解出符合条件的z,再代入
+
=b+i,利用复数相等的条件解出a,b的值,再由公式求w=a+bi的模
| a |
| z |
. |
| z |
解答:解:方程x2+2x+2=0的解x=-1±i,因为 Imz>0,所以z=-1+i,…(2分)
将z=-1+i代入
+
=b+i,得-(
+1)-(
+1)i=b+i,…(6分)
所以,
,…(8分) 解得
,所以w=-4+i,…(10分)
所以|w|=
,即复数w的模为
.…(12分)
将z=-1+i代入
| a |
| z |
. |
| z |
| a |
| 2 |
| a |
| 2 |
所以,
|
|
所以|w|=
| 17 |
| 17 |
点评:本题考查求得复数的模,复数相等的条件,解题的关键是熟练掌握复数求模的公式以及复数相等的条件,本题是复数中综合性较强的题

练习册系列答案
相关题目
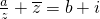 (其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.
(其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.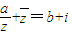 (其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.
(其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.