题目内容
已知复数z是方程x2+2x+5=0的解,且Imz<0,若
+
=b+i(其中a、b为实数,i为虚数单位,Imz表示z的虚部),求复数w=a+bi的模.
| a |
| z |
. |
| z |
分析:由方程结合题意可得z=-1-2i,代入已知由复数相等的定义可得ab的值,进而可得复数w,再由模长公式可得答案.
解答:解:方程x2+2x+5=0的解x=-1±2i,因为 Imz<0,所以z=-1-2i,
将z=-1-2i代入
+
=b+i,得
,
化简得
=-b+2+(-1-2b)i,
由复数相等的定义可得:
,
解得
,所以w=-
-
i,
所以|w|=
=
.
将z=-1-2i代入
| a |
| z |
. |
| z |
|
化简得
|
由复数相等的定义可得:
|
解得
|
| 5 |
| 2 |
| 1 |
| 2 |
所以|w|=
|
| ||
| 2 |
点评:本题考查复数的摸的运算,涉及复数的化简和复数相等的定义,属基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
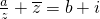 (其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.
(其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.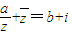 (其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.
(其中a、b为实数,i为虚数单位,Imz表示z的虚部).求复数w=a+bi的模.