题目内容
(本小题满分12) 如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4, ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点
(Ⅰ)求证: AC⊥BC1;
(Ⅱ)求二面角 的平面角的正切值.
的平面角的正切值.

【答案】
(Ⅰ)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,


∴ AC⊥BC, …………………1分
又 AC⊥ ,且
,且
∴ AC⊥平面BCC1 ,又 平面BCC1
……………………………………3分
平面BCC1
……………………………………3分
∴ AC⊥BC1 ………………………………………………………………4分
(Ⅱ)解法一:取 中点
中点 ,过
,过 作
作 于
于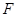 ,连接
,连接 …………5分
…………5分


 是
是 中点,
中点,
∴ ,又
,又 平面
平面
∴ 平面
平面 ,
,
又
 平面
平面 ,
, 平面
平面
∴
∴ 又
又
 且
且
∴ 平面
平面 ,
, 平面
平面 ………7分
………7分
∴ 又
又

∴ 是二面角
是二面角 的平面角 ……………………………………8分
的平面角 ……………………………………8分
 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,
∴在 中,
中, ,
, ,
,
∴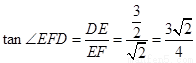 …………………………………………11分
…………………………………………11分
∴二面角 的正切值为
的正切值为 …………………………………………12分
…………………………………………12分
解法二:以 分别为
分别为 轴建立如图所示空间直角坐标系…………5分
轴建立如图所示空间直角坐标系…………5分

 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,
∴ ,
,
 ,
, ,
,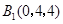 ,
,
∴ ,
,

平面 的法向量
的法向量 ,
…………………7分
,
…………………7分
设平面 的法向量
的法向量 ,
,
则 ,
, 的夹角(或其补角)的大小就是二面角
的夹角(或其补角)的大小就是二面角 的大小 …………8分
的大小 …………8分
则由 令
令 ,则
,则 ,
,
∴  ………………10分
………………10分
 ,则
,则 ……………11分
……………11分
∵二面角 是锐二面角
是锐二面角
∴二面角 的正切值为
的正切值为 …………………………
12分
…………………………
12分
【解析】略

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 内的随机点,求函数
内的随机点,求函数