题目内容
(本小题满分12分) 一几何体![]() 的三视图如图所示,
的三视图如图所示,![]() ,A1A=
,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() 在线段
在线段![]() 上且
上且![]() =
=![]() .
.
(I)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.

(I)见解析(II)![]()
解析:
方法一 :由三视图可知几何体是底面以![]() 为直角,侧棱
为直角,侧棱![]() 垂直底面的三棱台
垂直底面的三棱台![]() , ---------2分
, ---------2分
(I)证明 ∵A1A⊥平面ABC,BC![]() 平面ABC,
平面ABC,
∴A1A⊥BC.
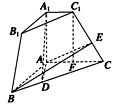 在Rt△ABC中,AB=
在Rt△ABC中,AB=![]() ,AC=2,∴BC=
,AC=2,∴BC=![]() .
.
∵BD∶DC=1∶2,∴BD=![]() .又
.又![]() =
=![]() =
=![]() ,
,
∴△DBA∽△ABC,∴∠ADB=∠BAC=90°,
即AD⊥BC.
又A1A∩AD=A,∴BC⊥平面A1AD.
∵BC![]() 平面BCC1B1,∴平面A1AD⊥平面BCC1B1. --------7分
平面BCC1B1,∴平面A1AD⊥平面BCC1B1. --------7分
(II)解 如图①,作AE⊥C1C交C1C于E点,连接BE,由已知得AB⊥平面ACC1A1,
∴AE是BE在平面ACC1A1内的射影.
由三垂线定理知BE⊥CC1,
∴∠AEB为二面角A—CC1—B的平面角. 图①
过C1作C1F⊥AC交AC于F点,
则CF=AC-AF=1,
C1F=A1A=![]() ,∴∠C1CF=60°.
,∴∠C1CF=60°.
在Rt△AEC中,
AE=ACsin60°=2×![]() =
=![]() ,
,
在Rt△BAE中,tan∠AEB=![]() =
=![]() =
=![]() ,
,
∴cos∠AEB=![]() ,
,
即二面角A—CC1—B余弦值为![]() -------12分
-------12分
方法二 (I) 证明 如图②,建立空间直角坐标系,
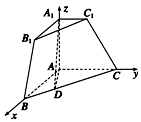
则A(0,0,0),B(![]() ,0,0),C(0,2,0),
,0,0),C(0,2,0),
A1(0,0,![]() ),C1(0,1,
),C1(0,1, ![]() ).
).
∵BD∶DC=1∶2,∴![]() =
=![]()
![]() ,
,
∴D点坐标为![]() ,
,
∴![]() =
=![]() ,
,![]() =(-
=(-![]() ,2,0),
,2,0),![]() =(0,0,
=(0,0,![]() ).
).
∵![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
∴BC⊥AA1,BC⊥AD.又A1A∩AD=A,
∴BC⊥平面A1AD.又BC![]() 平面BCC1B1,
平面BCC1B1,
∴平面A1AD⊥平面BCC1B1.
(II)解 ∵BA⊥平面ACC1A1,取m=![]() =(
=(![]() ,0,0)为平面ACC1A1的法向量.
,0,0)为平面ACC1A1的法向量.
设平面BCC1B1的法向量为n=(x,y,z),
则![]() ·n=0,
·n=0,![]() ·n=0,
·n=0,
∴![]()
∴x=![]() y,z=
y,z=![]() ,可取y=1,则n=
,可取y=1,则n=![]() ,
,
cos〈m,n〉=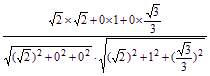
=![]() ,
,
即二面角A—CC1—B的余弦值为![]() .
.
