题目内容
1.$\frac{1+2i}{(1-i)^{2}}$=$-1+\frac{i}{2}$.分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:$\frac{1+2i}{(1-i)^{2}}$=$\frac{1+2i}{-2i}=\frac{(1+2i)i}{(-2i)•i}=\frac{-2+i}{2}=-1+\frac{i}{2}$.
故答案为:-1+$\frac{i}{2}$.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
11.在△ABC中,$a=7,b=4\sqrt{3},c=\sqrt{13}$,则△ABC的最小角为( )
| A. | 60° | B. | 30° | C. | 15° | D. | 45° |
11.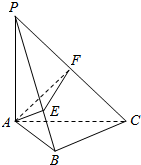 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
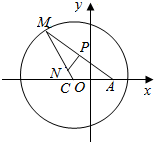 如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.
如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.