题目内容
若集合S={a, b, c} (a, b, c∈R)中三个元素为边可构成一个三角形,那么该三角形一定不可能是( )
| A.锐角三角形 | B.等腰三角形 | C.钝角三角形 | D.直角三角形 |
B
解析试题分析:根据集合中元素的互异性,可知a,b,c中任何两个数都不相等,因而不可能构成等腰三角形.
考点:本小题主要考查了集合元素的互异性.
点评:掌握集合元素的三条性质:唯一性,互异性,无序性是解决此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合 =( )
=( )
A. | B.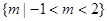 |
C.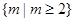 | D. |
方程组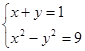 的解集是( )
的解集是( )
A.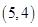 | B.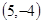 | C.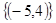 | D.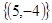 |
已知全集U=R,集合 ,则
,则 等于( )
等于( )
A.{ x ∣0 x x 2} 2} | B.{ x ∣0<x<2} |
| C.{ x ∣x<0或x>2} | D.{ x ∣x 0或x 0或x 2} 2} |
集合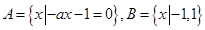 ,若
,若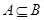 ,则实数
,则实数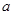 的取值的集合是( )
的取值的集合是( )
A.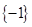 | B.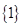 | C.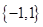 | D.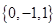 |
已知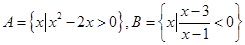 ,则
,则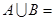 ( )
( )
A.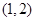 | B.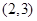 | C. | D.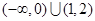 |
已知全集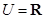 ,集合
,集合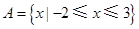 ,
,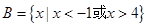 ,那么集合
,那么集合 ( )
( )
A. | B.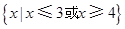 |
C.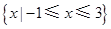 | D.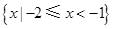 |
设全集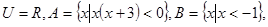 则右图中阴影部分表示的集合为( )
则右图中阴影部分表示的集合为( )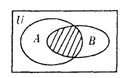
A.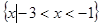 | B.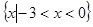 |
C.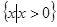 | D.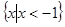 |
记集合
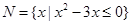 ,则
,则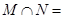
A. | B. |
C. | D.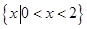 |