题目内容
设集合
=（ ）
A． | B． |
C． | D． |
C
解析试题分析： 因为集合根据一元二次不等式的解集和一元二次函数的性质知道，
那么可知答案选C.
考点：本题主要考查了集合的交集的运算问题。
点评：解决该试题的关键是利用一元二次不等式的解集来得到集合P,Q同时结合交集的概念得到结论。
练习册系列答案
阅读快车系列答案
相关题目
已知集合
={直线}，
={椭圆}，则
中元素个数为（ ）
| A．0 | B．1 | C．2 | D．0或1或2 |
已知A={x︱-1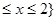
,B={x︱
},全集U=R,则
=( )
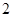A．{x︱ <x } | B．{x︱ } |
C．{x︱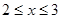 } | D．{x︱0<x} |
集合
，
,
,则
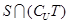等于（ ）
A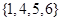． | B． |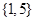
C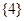． | D． |
已知集合
，则下列式子表示正确的有（ ）
①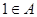
②
③
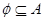④
| A．1个 | B．2个 | C．3个 | D．4个 |
已知全集
，设函数
的定义域为集合
，集合
，则
等于（ ）
A． | B． | C． | D． |
满足M
且
的集合M的个数是（ ）
| A．1 | B．２ | C．3 | D．4 |
若集合
，且
，则集合
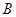可能是
A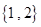． | B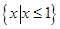． | C． | D．R |
若集合S={a, b, c} (a, b, c∈R)中三个元素为边可构成一个三角形，那么该三角形一定不可能是( )
| A．锐角三角形 | B．等腰三角形 | C．钝角三角形 | D．直角三角形 |