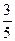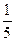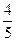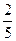题目内容
考虑一元二次方程x2+mx+n=0,其中m、n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
A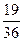． | B． | C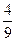． | D． |
A
由方程有实根知:m2≥4n.
由于n∈N*,故2≤m≤6.
骰子连掷两次并按先后所出现的点数考虑,共有6×6=36种情形.
其中满足条件的有:
①m=2,n只能取1,计1种情形;
②m=3,n可取1或2,计2种情形;
③m=4,n可取1或2、3、4,计4种情形;
④m=5或6,n均可取1至6的值,共计2×6=12种情形.
故满足条件的情形共有1+2+4+12=19(种).
由于n∈N*,故2≤m≤6.
骰子连掷两次并按先后所出现的点数考虑,共有6×6=36种情形.
其中满足条件的有:
①m=2,n只能取1,计1种情形;
②m=3,n可取1或2,计2种情形;
③m=4,n可取1或2、3、4,计4种情形;
④m=5或6,n均可取1至6的值,共计2×6=12种情形.
故满足条件的情形共有1+2+4+12=19(种).
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
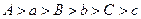
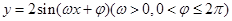，其中
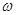是集合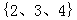
中任一元素，
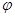是集合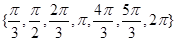
中任一元素.从这些函数中任意抽取两个，其图象能经过相同的平移后分别得到函数
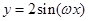的图象的概率是( )
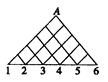
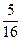
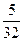
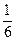
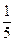
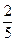
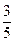
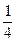
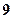个，其中
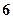个红色，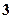
个黄色，现从中随机地摸
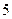分钟一班准时到达某车站，任一人在该车站等车少于
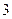分钟的概率（ ）。
