题目内容
已知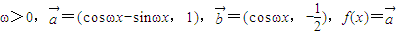 •
•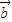 .
.(1)求函数f(x)的值域;
(2)若函数f(x)的相邻两条对称轴之间的距离为
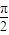 ,求f(x)在[0,π]上的单调区间.
,求f(x)在[0,π]上的单调区间.
【答案】分析:(1)先利用向量的数量积的坐标表示f(x)=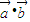 =
=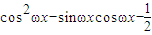 ,然后根据二倍角公式、辅助角公式对已知函数进行化简,结合正弦函数的性质即可求解
,然后根据二倍角公式、辅助角公式对已知函数进行化简,结合正弦函数的性质即可求解
(2)由周期公式可求ω,代入f(x)=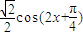 ,结合余弦函数的性质可求函数的单调区间
,结合余弦函数的性质可求函数的单调区间
解答:解:(1)由题意可得,f(x)=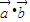 =
=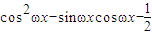
= cos2ωx-
cos2ωx-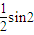 ωx=
ωx=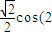 ωx+
ωx+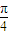 )
)
∴f(x)的值域为[-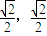 ]
]
(2)由题意可得,T=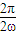 =π
=π
∴ω=1
∴f(x)=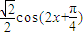
∵0≤x≤π
∴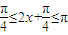 +2π
+2π
当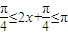 即
即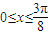 时,f(x)单调递减
时,f(x)单调递减
当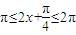 即
即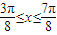 时,f(x)单调递增
时,f(x)单调递增
当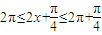 即
即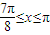 时,f(x)单调递减
时,f(x)单调递减
∴f(x)的单调递增区间[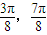 ],递减区间为[0,
],递减区间为[0,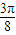 ],
],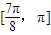
点评:本题主要考查了向量的数量积的坐标表示,二倍角公式、辅助角公式的应用,余弦函数的值域及单调性的求解
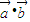 =
=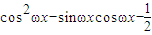 ,然后根据二倍角公式、辅助角公式对已知函数进行化简,结合正弦函数的性质即可求解
,然后根据二倍角公式、辅助角公式对已知函数进行化简,结合正弦函数的性质即可求解(2)由周期公式可求ω,代入f(x)=
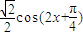 ,结合余弦函数的性质可求函数的单调区间
,结合余弦函数的性质可求函数的单调区间解答:解:(1)由题意可得,f(x)=
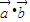 =
=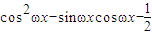
=
 cos2ωx-
cos2ωx-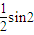 ωx=
ωx=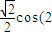 ωx+
ωx+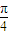 )
)∴f(x)的值域为[-
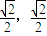 ]
](2)由题意可得,T=
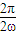 =π
=π∴ω=1
∴f(x)=
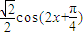
∵0≤x≤π
∴
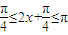 +2π
+2π当
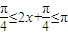 即
即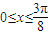 时,f(x)单调递减
时,f(x)单调递减当
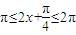 即
即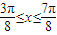 时,f(x)单调递增
时,f(x)单调递增当
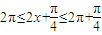 即
即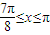 时,f(x)单调递减
时,f(x)单调递减∴f(x)的单调递增区间[
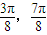 ],递减区间为[0,
],递减区间为[0,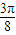 ],
],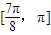
点评:本题主要考查了向量的数量积的坐标表示,二倍角公式、辅助角公式的应用,余弦函数的值域及单调性的求解

练习册系列答案
相关题目
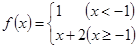 ,
,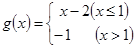 ,
,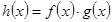
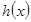 的解析式,并求它的单调递增区间;
的解析式,并求它的单调递增区间;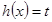 有四个不相等的实数根,求
有四个不相等的实数根,求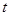 的取值范围。
的取值范围。 .
.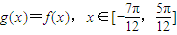 的图象,由图象研究并写出g(x)的对称轴和对称中心.
的图象,由图象研究并写出g(x)的对称轴和对称中心.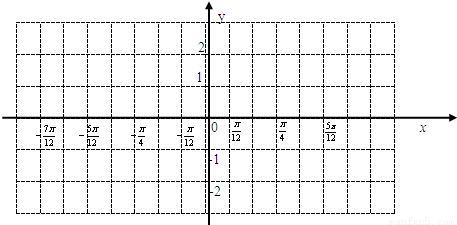
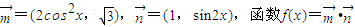 .
.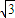 ,且a>b,求a,b的值.
,且a>b,求a,b的值. 是定义在
是定义在 上的偶函数,已知当
上的偶函数,已知当 时,
时, .
. 上的值域。
上的值域。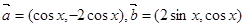 ,
,
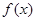 的最小正周期;
的最小正周期; ,求
,求