Question

已知，，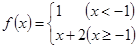 

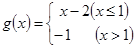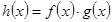
（1）求函数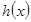的解析式，并求它的单调递增区间；

（2）若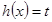有四个不相等的实数根，求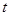的取值范围。

 

Answer 1

【答案】

（1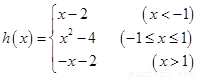），递增区间是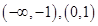；（2）．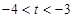

【解析】

试题分析：（1）由于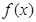与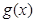都是分段函数，故在求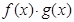时，要注意两个函数中不同的自变量的取值集合，单调区间当然要每段中都要考察；（2）方程有几个实根时，求参数的范围，一般可利用函数的图象求解．方程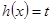的解可以看作是函数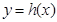的图象与直线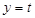的交点的横坐标，从而方程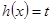有4个解等价于函数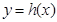的图象与直线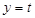有4个交点．

试题解析：（1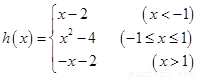）               5分

递增区间是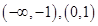2分

（2）如图所求，作出函数函数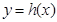的图象与直线 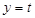              4分

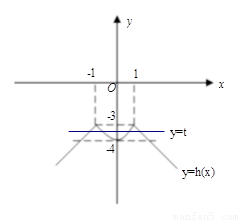
由图可得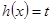有四个不相等的实数根时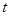的取值范围是 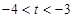             3分

考点：(1)分段函数的解析式，单调区间；（2）方程解的个数问题．