题目内容

如图1，在△ABC中，AB=3，AC=5，且O是△ABC的外心，则
AO
•
BC
的值是（　　）
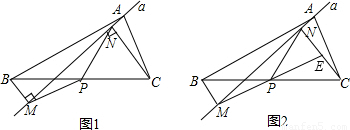
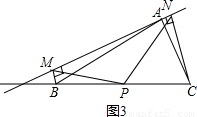
分析：如图所示，边AB、AC的垂直平分线分别为OM、ON，则|AO|cos∠OAM=
3
2
，|OA|cos∠OAC=
5
2
．再利用向量的运算法则即可得出．
解答：解：如图所示，边AB、AC的垂直平分线分别为OM、ON，
则|AO|cos∠OAM=
3
2
，|OA|cos∠OAC=
5
2
．
∴
AO
•
BC
=
AO
•(
AC
-
AB
)=
AO
•
AC
-
AO
•
AB

=5×|
AO
|cos∠OAC-3|
AO
|cos∠OAM=
25
2
-
9
2
=8．
故选D．
点评：熟练掌握三角形外心的性质、线段的垂直平分线的性质、向量的运算法则是解题的关键．
练习册系列答案
相关题目
如图1，在△ABC中AB⊥AC、AD⊥BC，D是垂足，则AB2=BD•BC（射影定理）．类似的有命题：在三棱锥A-BCD（图2）中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则（S△ABC）2=S△BCO•S△BCD（S表示面积．上述命题（　　）
如图1，在△ABC中，BC=3，AC=6，∠C=90°，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
精英家教网
（Ⅰ）求证：BC⊥平面A1DC；
（Ⅱ）若CD=2，求BE与平面A1BC所成角的正弦值．
如图1-9,在△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD交CB延长线于E,则结论正确的是(    )

图1-9

A.△AED∽△ACB                         B.△AEB∽△ACD

C.△BAE∽△ACE                         D.△AEC∽△DAC

如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若点B，P在直线a的异侧，BM⊥直线a于点M．CN⊥直线a于点N，连接PM，PN．

（1）延长MP交CN于点E（如图2）．

①求证：△BPM≌△CPE；

②求证：PM=PN；

（2）若直线a绕点A旋转到图3的位置时，点B，P在直线a的同侧，其它条件不变，此时PM=PN还成立吗？若成立，请给予证明；若不成立，请说明理由；

（3）若直线a绕点A旋转到与BC边平行的位置时，其它条件不变，请直接判断四边形MBCN的形状及此时PM=PN还成立吗？不必说明理由．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网