题目内容
如图,已知椭圆 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A。
交x轴于点K,左顶点为A。
 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A。
交x轴于点K,左顶点为A。
(Ⅰ)求证:KF平分∠MKN;
(Ⅱ)直线AM、AN分别交准线于点P、Q,设直线 MN的倾斜角为 ,试用
,试用 表示线段PQ的长度|PQ|,并求|PQ|的最小值。
表示线段PQ的长度|PQ|,并求|PQ|的最小值。
(Ⅱ)直线AM、AN分别交准线于点P、Q,设直线 MN的倾斜角为
 ,试用
,试用 表示线段PQ的长度|PQ|,并求|PQ|的最小值。
表示线段PQ的长度|PQ|,并求|PQ|的最小值。 (Ⅰ)证明:作MM1⊥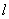 于M1,NN1⊥
于M1,NN1⊥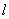 于N1,
于N1,
则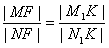 ,
,
又由椭圆的第二定义,有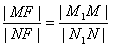 ,
,
∴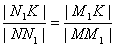 ,
,
∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴KF平分∠MKN。
(Ⅱ)解:由A,M,P三点共线可求出P点的坐标为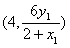 ,
,
由A,N,Q三点共线可求出Q点坐标为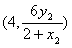 ,
,
设直线MN的方程为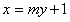 ,
,
由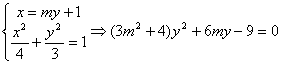 ,
,
∴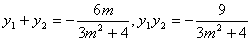 ,
,
则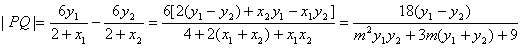
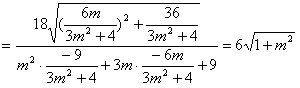 ,
,
又直线MN的倾斜角为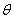 ,则
,则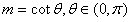 ,
,
∴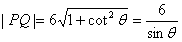 ,
,
即当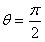 时,
时,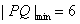 。
。
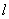 于M1,NN1⊥
于M1,NN1⊥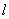 于N1,
于N1,则
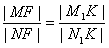 ,
,又由椭圆的第二定义,有
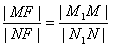 ,
,∴
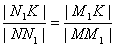 ,
,∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴KF平分∠MKN。
(Ⅱ)解:由A,M,P三点共线可求出P点的坐标为
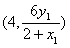 ,
,由A,N,Q三点共线可求出Q点坐标为
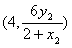 ,
,设直线MN的方程为
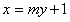 ,
,由
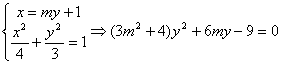 ,
,∴
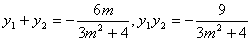 ,
,则
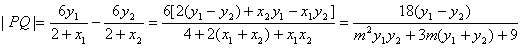
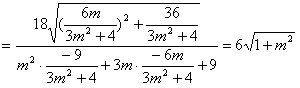 ,
,又直线MN的倾斜角为
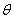 ,则
,则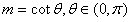 ,
,∴
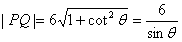 ,
,即当
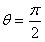 时,
时,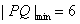 。
。
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:


