题目内容
已知e1,e2是两个单位向量,其夹角为θ,若向量m=2e1+3e2,则|m|=1的充要条件是( )
| A.θ=π | B.θ= |
C.θ= | D.θ=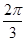 |
A
解析

练习册系列答案
相关题目
设P是△ABC所在平面内的一点, ,则( )
,则( )
A. | B. | C. | D. |
已知a与b均为单位向量,其夹角为 ,有下列四个命题
,有下列四个命题



其中的真命题是
A. | B. | C. | D.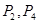 |
已知e1,e2是两个单位向量,其夹角为θ,若向量m=2e1+3e2,则|m|=1的充要条件是( )
| A.θ=π | B.θ= |
C.θ= | D.θ= |
已知两个非零向量a,b满足|a+b|=|a-b|,则下面结论正确的是( )
| A.a∥b | B.a⊥b |
| C.|a|=|b| | D.a+b=a-b |
已知O是△ABC所在平面内一点,D为BC边中点,且2 +
+ +
+ =0,那么( )
=0,那么( )
A. = = | B. =2 =2 |
C. =3 =3 | D.2 = = |
在平面斜坐标系xOy中∠xOy=45°,点P的斜坐标定义为:若 =x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足|
=x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足|  |=|
|=| |,则点M在斜坐标系中的轨迹方程为( )
|,则点M在斜坐标系中的轨迹方程为( )
A.x- y=0 y=0 | B.x+ y=0 y=0 | C. x-y=0 x-y=0 | D. x+y=0 x+y=0 |
若M为△ABC所在平面内一点,且满足( -
- )·(
)·( +
+ -2
-2  )=0,则△ABC为( ).
)=0,则△ABC为( ).
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.等腰直角三角形 |
 ,
, ,定义一种向量积:
,定义一种向量积: .已知向量
.已知向量 ,
, ,点P在
,点P在 的图象上运动,点Q在
的图象上运动,点Q在 的图象上运动,且满足
的图象上运动,且满足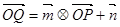 (其中O为坐标原点),则
(其中O为坐标原点),则 上的最大值是( )
上的最大值是( )


