题目内容
在平面斜坐标系xOy中∠xOy=45°,点P的斜坐标定义为:若 =x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足|
=x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足|  |=|
|=| |,则点M在斜坐标系中的轨迹方程为( )
|,则点M在斜坐标系中的轨迹方程为( )
A.x- y=0 y=0 | B.x+ y=0 y=0 | C. x-y=0 x-y=0 | D. x+y=0 x+y=0 |
D
解析

练习册系列答案
相关题目
在平面直角坐标系 中,点
中,点 和点
和点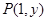 满足:向量
满足:向量 在向量
在向量 上的投影为
上的投影为 ,则
,则 的值为( )
的值为( )
| A.5 | B. | C.8 | D. |
设 、
、 是两个非零向量,则使
是两个非零向量,则使 成立的一个必要非充分的条件是( )
成立的一个必要非充分的条件是( )
A. | B. | C. | D. |
已知向量 满足
满足 ,则向量
,则向量 的夹角为 ( )
的夹角为 ( )
A. | B. | C. | D. |
已知 和点
和点 满足
满足
 .若存在实数
.若存在实数 使得
使得 成立,则
成立,则 =( )
=( )
| A. 2 | B. 3 | C. 4 | D. 5 |
已知 则
则 是钝角三角形的概率为 ( )
是钝角三角形的概率为 ( )
A. | B. | C. | D. |
已知e1,e2是两个单位向量,其夹角为θ,若向量m=2e1+3e2,则|m|=1的充要条件是( )
| A.θ=π | B.θ= |
C.θ= | D.θ=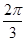 |
在△ABC中, =2
=2 ,
, =m
=m +n
+n ,则
,则 的值为( )
的值为( )
| A.2 | B. | C.3 | D. |
已知点A(1,3),B(4,-1),则与向量 同方向的单位向量为( ).
同方向的单位向量为( ).
A. | B. |
C. | D. |