题目内容

已知双曲线C：
x2
a2
-
y2
b2
=1（a，b为大于0的常数），过第一象限内双曲线上任意一点P作切线l，过原点作l的平行线交PF1于M，则|MP|=
a
a
（用a，b表示）．
分析：设双曲线的右端点为A，考察特殊情形，当点P趋近于A时，切线l趋近于直线x=a，此时|PM|趋近于|AO|，即|PM|趋近于a，从而得出答案．
解答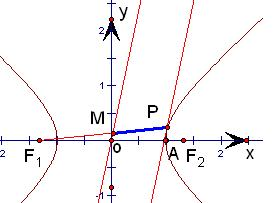：解：考察特殊情形，设双曲线的右端点为A，
当点P趋近于A时，
切线l就趋近于直线x=a，
此时|PM|趋近于|AO|，
即|PM|趋近于a，
特别地，当P与A重合时，|PM|=a．
运用合情推理，得出结论|MP|=a．
故答案为：a．
点评：本小题主要考查双曲线的简单性质、双曲线的标准方程等基础知识，考查数形结合思想、极限思想．属于基础题．
练习册系列答案
相关题目
（2013•许昌三模）已知双曲线c：
x2
a
-
y2
b
=1（a＞．，b＞0）的半焦距为c，过左焦点且斜率为1的直线与双曲线C的左、右支各有一个交点，若抛物线y2=4cx的准线被双曲线截得的线段长大于
2
2
3
be2．（e为双曲线c的离心率），则e的取值范同是
（
2
，
3
）
（
2
，
3
）
．
（2009•宁波模拟）已知双曲线
x2
a
-
y2
a2+a+1
=1的离心率的范围是数集M，设p：“k∈M”； q：“函数f（x）=
lg
x-1
x-2
  x＜1
2x-k       x≥1
的值域为R”．则P是Q成立的（　　）
已知双曲线
x2
a
-
y2
a2+a+1
=1的离心率的范围是数集M，设p：“k∈M”； q：“函数f（x）=
lg
x-1
x-2
  x＜1
2x-k       x≥1
的值域为R”．则P是Q成立的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
已知双曲线c：
x2
a
-
y2
b
=1（a＞．，b＞0）的半焦距为c，过左焦点且斜率为1的直线与双曲线C的左、右支各有一个交点，若抛物线y2=4cx的准线被双曲线截得的线段长大于
2
2
3
be2．（e为双曲线c的离心率），则e的取值范同是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网