题目内容
(本小题满分12分)数列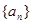 的前n项和为
的前n项和为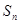 ,
,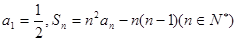
(1)求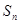 关于n的表达式;
关于n的表达式;
(2)设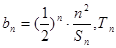 为数列
为数列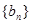 的前n项和,试比较
的前n项和,试比较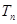 与
与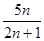 的大小,并加以证明
的大小,并加以证明
【答案】
(1)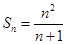
(2) 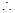 当
当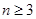 时,有
时,有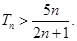 证明略
证明略
【解析】解:(1)当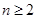 时,
时,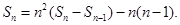 即
即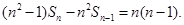
于是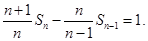
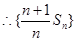 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。
从而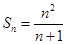 .………………6分
.………………6分
(2)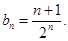 则
则 ,
,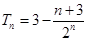 。…………9分
。…………9分
 显然:当
显然:当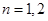 时,有
时,有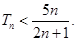
当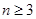 时,
时,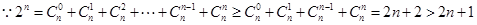
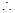 当
当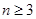 时,有
时,有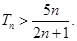 …………………..12分
…………………..12分

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目