题目内容
16．函数f（x）=lg$\frac{1+x}{1-x}$（其中x≠±1）是（ ）函数．| A． | 奇 | B． | 偶 | C． | 既奇又偶 | D． | 非奇非偶 |
分析 根据奇函数的定义，先可求出定义域为（-1，1），然后根据对数的运算可以求出f（-x）=-f（x），从而便可判断f（x）为奇函数．
解答 解：解$\frac{1+x}{1-x}＞0$得，-1＜x＜1；
f（-x）=$lg\frac{1-x}{1+x}=-lg\frac{1+x}{1-x}$=-f（x）；
∴f（x）为奇函数．
故选：A．
点评 考查奇函数的定义，判断奇函数的方法：求定义域，求f（-x），以及对数的运算．
练习册系列答案
相关题目
7．
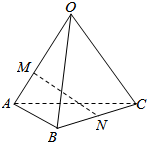如图，空间四边形OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$，点N为BC中点，则$\overrightarrow{MN}$等于（ ）
如图，空间四边形OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$，点N为BC中点，则$\overrightarrow{MN}$等于（ ）| A． | $\frac{1}{2}\vec a-\frac{2}{3}\vec b+\frac{1}{2}\vec c$ | B． | $-\frac{2}{3}\vec a+\frac{1}{2}\vec b+\frac{1}{2}\vec c$ | C． | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\frac{1}{2}\vec c$ | D． | $\frac{2}{3}\vec a+\frac{2}{3}\vec b-\frac{1}{2}\vec c$ |
11．将$\root{3}{2^2}$化成分数指数幂为（ ）
| A． | ${2^{\frac{3}{2}}}$ | B． | $2^{-\frac{1}{2}}$ | C． | $2^{\frac{1}{3}}$ | D． | $2^{\frac{2}{3}}$ |
8．顶点在x轴上，两顶点间的距离为4，离心率e=$\frac{\sqrt{5}}{2}$的双曲线与直线y=kx（k∈R）无交点，则实数k的取值范围为（ ）
| A． | [-$\frac{1}{2}$，$\frac{1}{2}$] | B． | （-∞，-$\frac{1}{2}$]∪[$\frac{1}{2}$，∞） | C． | （-$\frac{1}{2}$，$\frac{1}{2}$） | D． | （-∞，-$\frac{1}{2}$）∪（$\frac{1}{2}$，+∞） |