题目内容
已知圆C的圆心在直线y=x+1上,且过点A(1,3),与直线x+2y-7=0相切。
(1)求圆C的方程;
(2)设直线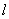 :
: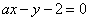
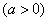 与圆C相交于A、B两点,求实数a的取值范围;
与圆C相交于A、B两点,求实数a的取值范围;
(3)在(2)的条件下,是否存在实数a,使得弦AB的垂直平分线过点P(-2,4), 若存在,求出实数a的值;若不存在,请说明理由。
(1)求圆C的方程;
(2)设直线
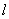 :
: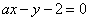
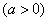 与圆C相交于A、B两点,求实数a的取值范围;
与圆C相交于A、B两点,求实数a的取值范围;(3)在(2)的条件下,是否存在实数a,使得弦AB的垂直平分线过点P(-2,4), 若存在,求出实数a的值;若不存在,请说明理由。
解:(1)圆C的方程为 ;
;
(2)把直线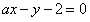 即
即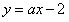 代入圆的方程,
代入圆的方程,
消去y整理,得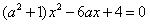 ,
,
由于直线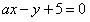 交圆于A,B两点,
交圆于A,B两点,
故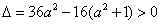 ,即
,即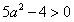 ,
,
由于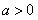 ,解得
,解得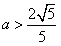 ,
,
所以实数a的取值范围是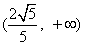 。
。
(3)设符合条件的实数a存在,由于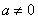 ,则直线
,则直线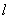 的斜率为
的斜率为 ,
,
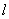 的方程为
的方程为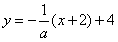 , 即
, 即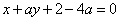 ,
,
由于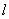 垂直平分弦AB,故圆心M(0,1)必在
垂直平分弦AB,故圆心M(0,1)必在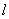 上,
上,
所以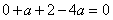 ,解得
,解得 ,
,
由于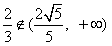 ,
,
故不存在实数a,使得过点P(-2,4)的直线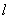 垂直平分弦AB。
垂直平分弦AB。
 ;
;(2)把直线
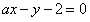 即
即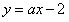 代入圆的方程,
代入圆的方程,消去y整理,得
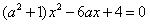 ,
,由于直线
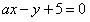 交圆于A,B两点,
交圆于A,B两点,故
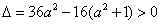 ,即
,即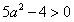 ,
,由于
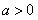 ,解得
,解得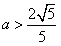 ,
,所以实数a的取值范围是
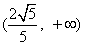 。
。(3)设符合条件的实数a存在,由于
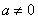 ,则直线
,则直线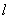 的斜率为
的斜率为 ,
,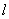 的方程为
的方程为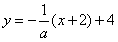 , 即
, 即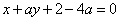 ,
,由于
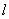 垂直平分弦AB,故圆心M(0,1)必在
垂直平分弦AB,故圆心M(0,1)必在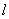 上,
上,所以
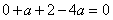 ,解得
,解得 ,
,由于
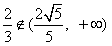 ,
,故不存在实数a,使得过点P(-2,4)的直线
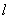 垂直平分弦AB。
垂直平分弦AB。
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目