题目内容
函数y=3sinx+
cosx（-
≤x≤）的值域是________．
[-3，2]
分析：直接利用两角和的正弦函数，化简函数的表达式为一个角的一个三角函数的形式，通过x的范围求出函数的值域．
解答：函数y=3sinx+cosx=2sin（x+
），
又-≤x≤，
所以x+∈[
]，
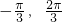∴sin（x+）
，
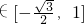∴2sin（x+）∈[-3，2]，
故答案为：[-3，2]．
点评：本题是基础题，考查三角函数的化简求值，值域x的范围与正弦函数的值域，是今天的关键，考查计算能力．
]分析：直接利用两角和的正弦函数，化简函数的表达式为一个角的一个三角函数的形式，通过x的范围求出函数的值域．
解答：函数y=3sinx+
cosx=2sin（x+），又-
≤x≤，所以x+
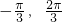∈[]，∴sin（x+
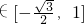），∴2
sin（x+）∈[-3，2]，故答案为：[-3，2
]．点评：本题是基础题，考查三角函数的化简求值，值域x的范围与正弦函数的值域，是今天的关键，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=3sinx+4cosx+5的最小正周期是（ ）
A、
| ||
B、
| ||
| C、π | ||
| D、2π |