题目内容
下面有四个命题:
①函数y=sin4x-cos4x的最小正周期是π;
②函数y=3sinx+4cosx的最大值是5;
③把函数y=3sin(2x+
)的图象向右平移
得y=3sin2x的图象;
④函数y=sin(x-
)在(0,π)上是减函数.
其中真命题的序号是
①函数y=sin4x-cos4x的最小正周期是π;
②函数y=3sinx+4cosx的最大值是5;
③把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
④函数y=sin(x-
| π |
| 2 |
其中真命题的序号是
①②③
①②③
.分析:①将三角函数进行化简,利用周期公式求函数的周期.②利用辅助角公式求函数的最大值.③利用函数的平移关系求函数的解析式.④利用三角函数的性质判断.
解答:解:①因为y=sin4x-cos4x=(sin2x+cos2x)(sin2x-cos2x)=-cos2x,所以函数的周期T=
=π,所以①正确.
②因为y=3sinx+4cosx=5(
sin?x+
cos?x),令cos?θ=
,sin?θ=
,则y=5sin(x+θ),所以函数的最大值是5,所以②正确.
③把函数y=3sin(2x+
)的图象向右平移
得到y=3sin[2(x-
)+
]=3sin2x,所以③正确.
④因为y=sin(x-
)=-cosx,所以在(0,π)上函数单调递增,所以④错误.
故答案为:①②③.
| 2π |
| 2 |
②因为y=3sinx+4cosx=5(
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
③把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
④因为y=sin(x-
| π |
| 2 |
故答案为:①②③.
点评:本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的性质和三角公式.考查学生的运算能力.

练习册系列答案
相关题目
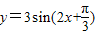 的图象向右平移
的图象向右平移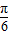 得y=3sin2x的图象;
得y=3sin2x的图象;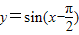 在(0,π)上是减函数.
在(0,π)上是减函数.