题目内容
2.已知半圆的直径AB=10,O为圆心,C为半圆上不同于A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )| A. | $\frac{25}{2}$ | B. | -25 | C. | 25 | D. | -$\frac{25}{2}$ |
分析 画出图形,讨论P点的位置:P点在O点和C点时,容易求出$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}=0$,而P点在O,C之间时,将$\overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PO}$带入,根据基本不等式便可得到$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}≥-2•(\frac{25}{4})$,最后即可得到$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}$的最小值.
解答 解:如图,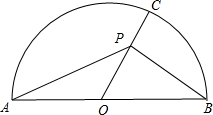 (1)若点P和O重合,则:$\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}$;
(1)若点P和O重合,则:$\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}$;
∴$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}=0$;
(2)若点P和C重合,则$\overrightarrow{PC}=\overrightarrow{0}$;
∴$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}=0$;
(3)若点P在O,C之间,则:$\overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PO}$;
∴$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}=2\overrightarrow{PO}•\overrightarrow{PC}$=$-2|\overrightarrow{PO}||\overrightarrow{PC}|$;
$|\overrightarrow{PO}|>0,|\overrightarrow{PC}|>0$;
∴$|\overrightarrow{PO}||\overrightarrow{PC}|≤(\frac{|\overrightarrow{PO}|+|\overrightarrow{PC}|}{2})^{2}=\frac{25}{4}$;
∴$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}≥-\frac{25}{2}$;
综上得$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}$的最小值为$-\frac{25}{2}$.
故选D.
点评 考查对零向量的理解,向量加法的平行四边形法则,数量积的计算公式,以及基本不等式:a+b$≥2\sqrt{ab}$,a>0,b>0.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案| A. | x1>x2 | B. | x1<x2 | C. | |x1|<|x2| | D. | |x1|>|x2| |

| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | 0 | D. | $\sqrt{3}$ |